
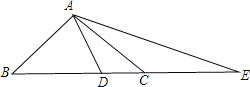
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
【答案】(1)450;(2)不改变;(3)∠DAE=![]() ∠BAC.
∠BAC.
【解析】
(1)要求∠DAE,必先求∠BAD和∠CAE,由∠BAC=90°,AB=AC,可求∠B=∠ACB=45°,又因为BD=BA,可求∠BAD=∠BDA=67.5°,再由CE=CA,可求∠CAE=∠E=22.5°,所以∠DAE=∠BAE-∠BAD=112.5°-67.5°=45°;
(2)先设∠CAE=x,由已知CA=CE可求∠ACB=∠CAE+∠E=2x,∠B=90°-2x,又因为BD=BA,所以∠BAD=∠BDA=x+45°,再根据三角形的内角和是180°,可求∠BAE=90°+x,即∠DAE=∠BAE-∠BAD=(90°+x)-(x+45°)=45度;
(3)可设∠CAE=x,∠BAD=y,则∠B=180°-2y,∠E=∠CAE=x,所以∠BAE=180°-∠B-∠E=2y-x,∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x,即∠DAE=![]() ∠BAC.
∠BAC.
(1)∵AB=AC,∠BAC=![]() ,
,
∴∠B=∠ACB=![]() ,
,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180∠B)=
(180∠B)=![]()
∵CE=CA,
∴∠CAE=∠E=![]() ∠ACB=
∠ACB=![]() ,
,
在△ABE中,∠BAE=180∠B∠E=![]() ,
,
∴∠DAE=∠BAE∠BAD=![]()
![]() =
=![]() ;
;
(2)不改变.
设∠CAE=x,
∵CA=CE,
∴∠E=∠CAE=x,
∴∠ACB=∠CAE+∠E=2x,
在△ABC中,∠BAC=![]() ,
,
∴∠B=![]() ∠ACB=
∠ACB=![]() 2x,
2x,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180∠B)=x+
(180∠B)=x+![]() ,
,
在△![]() ∠B∠E,=
∠B∠E,=![]() (
(![]() 2x)x=
2x)x=![]() +x,
+x,
∴∠DAE=∠BAE∠BAD,=(![]() +x)(x+
+x)(x+![]() )=
)=![]() ;
;
(3)∠DAE=![]() ∠BAC.
∠BAC.
理由:设∠CAE=x,∠BAD=y,
则∠B=![]() 2y,∠E=∠CAE=x,
2y,∠E=∠CAE=x,
∴∠BAE=![]() ∠B∠E=2yx,
∠B∠E=2yx,
∴∠DAE=∠BAE∠BAD=2yxy=yx,
∠BAC=∠BAE∠CAE=2yxx=2y2x,
∴∠DAE=![]() ∠BAC.
∠BAC.


科目:初中数学 来源: 题型:
【题目】如图所示,△ABC与点O在10×10的网格中的位置如图所示 
(1)画出△ABC绕点O逆时针旋转90°后的图形;
(2)画出△ABC绕点O逆时针旋转180°后的图形;
(3)若⊙M能盖住△ABC,则⊙M的半径最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() = ; (2)
= ; (2)![]() = ; (3)
= ; (3)![]() ;
;
(4)![]() ; (5)
; (5)![]() ; (6)a3·a3= ;
; (6)a3·a3= ;
(7) (x3)5= ; (8)(-2x2y3)3= ; (9) (x-y)6÷(x-y)3= ;
(10)a2b(ab-4b2) (11)(2a-3b)(2a+5b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(4)连接AC,H是抛物线上一动点,过点H作AC的平行线交x轴于点F.是否存在这样的点F,使得以A,C,H,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
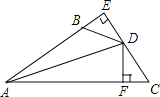
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,AB=12,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
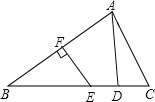
(1)求证:AD⊥BC.
(2)若∠BAC=75°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C两点同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止,点Q以2cm/s的速度向点D移动.
(1)P、Q两点从出发开始,经过几秒时,四边形PBCQ的面积为33cm2?
(2)P、Q两点从出发开始,经过几秒时,点P和点Q的距离为10cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com