练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点P是AB上任一点，∠ABC=∠ABD，从下列各条件中补充一个条件，不一定能推出ΔAPC≌ΔAPD的是（ ）

    A．BC=BD B．∠ACB=∠ADB C．AC=AD D．∠CAB=∠DAB

    【答案】C

    【解析】

    试题分析：选项A，补充BC=BD，利用SAS先证出△ABC≌△ABD，可得∠CAB=∠DAB，AC=AD，再利用SAS即可得△APC≌△APD，选项A正确；选项B，补充∠ACB=∠ADB，利用AAS先证出△ABC≌△ABD，可得∠CAB=∠DAB，AC=AD，再利用SAS即可得△APC≌△APD，选项B正确；选项C，补充AC=AD，不能推出△APC≌△APD，选项C错误；选项D，补充∠CAB=∠DAB，利用ASA先证出△ABC≌△ABD，可得AC=AD，再利用SAS即可得△APC≌△APD，选项D正确．故答案选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB的垂直平分线EF交BC于点E，交AB于点F，D为线段CE的中点，BE=AC．

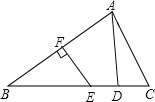
    （1）求证：AD⊥BC．

    （2）若∠BAC=75°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】八年级(3)班共有学生54人，学习委员调查了班级学生参加课外活动的情况(每人只参加一项活动)，其中：参加读书活动的18人，参加科技活动的人数占全班总人数的，参加艺术活动的比参加科技活动的多3人，所调查班级同学参加体育活动情况如图所示，则在扇形图中表示参加体育活动人数的扇形的圆心角大小为(　　)

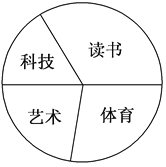
    A. 100° B. 110°

    C. 120° D. 130°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小强掷两枚质地均匀的骰子，每个骰子的六个面上分别刻有1到6的点数，则两枚骰子点数相同的概率为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知E是正方形ABCD的边CD的中点，点F在BC上，且∠DAE=∠FAE，

    求证：AF=AD+CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB=4cm，AC=BD=3cm．∠CAB=∠DBA=60°，点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s），则点Q的运动速度为 cm/s，使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．E、F分别是BC、CD上的点．且∠EAF＝60°．探究图中线段BE、EF、FD之间的数量关系．

    小王同学探究此问题的方法是，延长FD到点G，使DG＝BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是　 　；

    探索延伸：

    如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°．E、F分别是BC、CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由；

    实际应用：

    如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据题意解答
    （1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得线段BE、EF、FD之间的数量关系为 ．

    （2）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF= ∠BAD，线段BE、EF、FD之间存在什么数量关系，为什么？

    （3）如图3，点A在点O的北偏西30°处，点B在点O的南偏东70°处，且AO=BO，点A沿正东方向移动249米到达E处，点B沿北偏东50°方向移动334米到达点F处，从点O观测到E、F之间的夹角为70°，根据（2）的结论求E、F之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】九年级三班学生苏琪为帮助同桌万宇巩固“平面直角坐标系四个象限内及坐标轴上的点的坐标特点”这一基础知识，在三张完全相同且不透明的卡片正面分别写上了﹣3，0，2三个数字，背面向上洗匀后随机抽取一张，将卡片上的数字记为a，再从剩下的两张中随机取出一张，将卡片上的数字记为b，然后叫万宇在平面直角坐标系中找出点M（a，b）的位置．
    （1）请你用树状图帮万宇同学进行分析，并写出点M所有可能的坐标；
    （2）求点M在第二象限的概率；
    （3）张老师在万宇同学所画的平面直角坐标系中，画了一个半径为3的⊙O，过点M能作多少条⊙O的切线？请直接写出答案．

    查看答案和解析>>

    同步练习册答案