
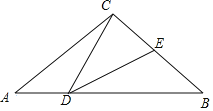
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() ,
,![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交
交![]() 于点
于点![]() .若
.若![]() 是等腰三角形,则
是等腰三角形,则![]() 的度数是____.
的度数是____.
【答案】80°或110°
【解析】
分类讨论:当CD=DE时;当DE=CE时;当EC=CD时;然后利用等腰三角形的性质和三角形的内角和定理进行计算.
解:分三种情况:
①当CD=DE时,
∵∠CDE=40°,
∴∠DCE=∠DEC=70°,
∴∠ADC=∠B+∠DCE=110°;
②当DE=CE时,
∵∠CDE=40°,
∴∠DCE=∠CDE=40°,
∴∠ADC=∠DCE+∠B=80°;
③当EC=CD时,
∠BCD=180°-∠CED-∠CDE=180°-40°-40°=100°,
∵∠ACB=100°,
∴此时,点D与点A重合,不合题意.
综上所述,若△CDE是等腰三角形,则∠ADC的度数为80°或110°.
故答案为:80°或110°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣![]() 与 是关于1的平衡数;
与 是关于1的平衡数;
(2)若(m+![]() )×(1﹣
)×(1﹣![]() )=﹣5+3
)=﹣5+3![]() ,判断m+
,判断m+![]() 与5﹣
与5﹣![]() 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读材料:实数的整数部分与小数部分
由于实数的小数部分一定要为正数,所以正、负实数的整数部分与小数部分确定方法存在区别:
⑴对于正实数,如实数9.23,在整数9—10之间,则整数部分为9,小数部分为9.23-9=0.23.
⑵对于负实数,如实数-9.23,在整数-10—-9之间,则整数部分为-10,小数部分为-9.23-(-10)=0.77.依照上面规定解决下面问题:
(1)已知![]() 的整数部分为a,小数部分为b,求a、b的值.
的整数部分为a,小数部分为b,求a、b的值.
(2)若x、y分别是8-![]() 的整数部分与小数部分,求
的整数部分与小数部分,求![]() 的值.
的值.
(3)设x=![]() , a是x的小数部分,b是 - x的小数部分.求
, a是x的小数部分,b是 - x的小数部分.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
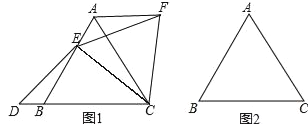
【题目】如图,已知△ABC是等边三角形.
(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
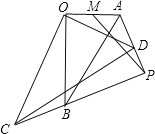
【题目】如图,Rt△AOB∽Rt△DOC,∠ABO=30°,∠AOB=∠COD=90°,M为OA的中点,OA=4,将△COD绕点O旋转一周,直线AD,CB交于点P,连接MP,则MP的最小值是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com