
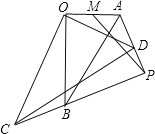
【题目】如图,Rt△AOB∽Rt△DOC,∠ABO=30°,∠AOB=∠COD=90°,M为OA的中点,OA=4,将△COD绕点O旋转一周,直线AD,CB交于点P,连接MP,则MP的最小值是_________.
【答案】4-2![]()
【解析】
根据相似三角形的判定定理证明△COB∽△DOA,得到∠OBC=∠OAD,得到∠APB=∠AOB=90°,求出MS和PS,根据三角形三边关系解答即可.
如图:
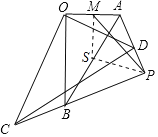
取AB的中点S,连接MS、PS,
则PS-MS≤PM≤MS+PS,
∵∠AOB=90°,OA=4,∠ABO=30°,
∴AB=2OA=8,OB=4![]() ,
,
∵∠AOB=∠COD=90°,
∴∠COB=∠DOA,
∵△AOB∽△DOC,
∴![]() ,
,
∴△COB∽△DOA,
∴∠OBC=∠OAD,
∵∠OBC+∠PBO=180°,
∴∠OAD+∠PBO=180°,∠AOB+∠APB=180°,
∴∠APB=∠AOB=90°,又S是AB的中点,
∴PS=![]() AB=4,
AB=4,
∵M为OA的中点,S是AB的中点,
∴MS=![]() OB=
OB=![]() ,
,
∴MP的最小值为4-![]() ,
,
故答案为:4-![]() .
.


科目:初中数学 来源: 题型:
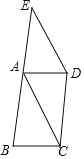
【题目】如图,已知四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接DE,AC
(1)求证:四边形ACDE为平行四边形;
(2)连接CE交AD于点O,若AC=AB=3,cosB=![]() ,求线段CE的长.
,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD,添加下列条件不能使四边形ABCD成为平行四边形的是( )
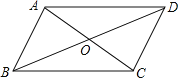
A.AB=CDB.OB=OD
C.∠BCD+∠ADC=180°D.AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为![]() .
.
(1)求线段AP的长;
(2)若DE是⊙O的切线,求线段OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com