【题目】如图，在四边形ABCD中，对角线AC，BD相交于点O，AB∥CD，添加下列条件不能使四边形ABCD成为平行四边形的是（ ）
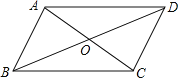
A.AB＝CDB.OB＝OD
C.∠BCD+∠ADC＝180°D.AD＝BC
【答案】D
【解析】
已知AB∥CD，可根据有一组边平行且相等的四边形是平行四边形来判定，也可根据两组对边分别平行的四边形是平行四边形来判定．
∵在四边形ABCD中，AB∥CD，
∴可添加的条件是：AB＝CD，
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形），故选项A不符合题意；
∵AB∥CD，
∴∠ABD＝∠CDB，
在△AOB和△COD中
，
∴△AOB≌△COD（ASA），
∴AB＝CD，
∴四边形ABCD为平行四边形，故选项B不符合题意；
∵∠BCD+∠ADC＝180°，
∴AD∥BC，
∵AB∥CD，
∴四边形ABCD是平行四边形，故选项C不符合题意；
∵AB∥CD，AD＝BC无法得出四边形ABCD是平行四边形，故选项D符合题意．
故选：D．
科目：初中数学 来源： 题型：
【题目】有四张正面分别标有数字2，1，﹣3，﹣4的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上，洗匀后从四张卡片中随机地摸取一张不放回，将该卡片上的数字记为m，再随机地摸取一张，将卡片上的数字记为n．
（1）请画出树状图并写出（m，n）所有可能的结果；
（2）求所选出的m，n能使一次函数y=mx+n的图象经过第二、三、四象限的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】给出如下定义：对于⊙O 的弦 MN 和⊙O 外一点 P（M，O，N 三点不共线，且点 P，O 在直线 MN 的异侧），当∠MPN+∠MON=180°时，则称点 P 是线段 MN 关于点 O 的关联点．图 1 是点 P 为线段 MN 关于点 O 的关联点的示意图．
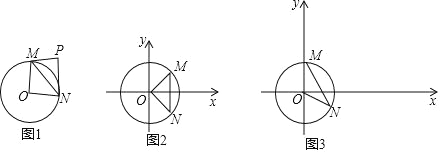
在平面直角坐标系 xOy 中，⊙O 的半径为 1．
（1）如图 2，已知 M（
，），N（ ，﹣），在 A（1，0），B（1，1），C（
，0）三点中，是线段 MN 关于点 O 的关联点的是哪个点；
（2）如图 3，M（0，1），N（
，﹣
），点 D 是线段 MN 关于点 O 的关联点．
①求∠MDN 的大小；
②在第一象限内有一点 E（
m，m），点 E 是线段 MN 关于点 O 的关联点，判断△MNE 的形状，并直接写出点 E 的坐标；
③点 F 在直线 y=﹣
x+2 上，当∠MFN≥∠MDN 时，求点 F 的横坐标 x 的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与
轴、
轴分别相交于点A和B.
（1）直接写出坐标：点A ，点B ；
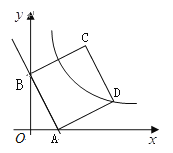
（2）以线段AB为一边在第一象限内作□ABCD，其顶点D(
， 
)在双曲线
(
＞
)上.
①求证：四边形ABCD是正方形；
②试探索：将正方形ABCD沿
轴向左平移多少个单位长度时，点C恰好落在双曲线
(
＞
)上.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△AOB∽Rt△DOC，∠ABO＝30°，∠AOB＝∠COD＝90°，M为OA的中点，OA＝4，将△COD绕点O旋转一周，直线AD，CB交于点P，连接MP，则MP的最小值是_________．
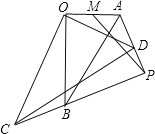
查看答案和解析>>
科目：初中数学 来源： 题型：
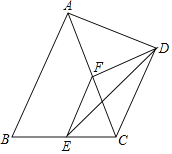
【题目】如图，在△ABC中，AB＝AC，E，F分别是BC，AC的中点，以AC为斜边作Rt△ADC，若∠CAD＝∠BAC＝45°，则下列结论：①CD∥EF；②EF＝DF；③DE平分∠CDF；④∠DEC＝30°；⑤AB＝
CD；其中正确的是_____（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠C=90°，∠A=30°．
（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E．（保留作图痕迹，不要求写作法和证明）；
（2）连接BD，求证：BD平分∠CBA．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
