
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
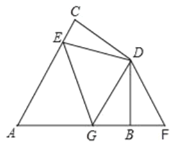
(1)试说明:![]() ;
;
(2)在图中,若点![]() 在
在![]() 上,且
上,且![]() ,试猜想
,试猜想![]() 、
、![]() 、
、![]() 之间的数量关系,并证明所归纳结论.
之间的数量关系,并证明所归纳结论.
【答案】(1)见解析;(2)![]() ,证明见解析
,证明见解析
【解析】
(1)通过角的计算得出∠C=∠DBF,结合CD=BD、CE=BF即可证出△CDE≌△BDF(SAS),由此即可得出DE=DF;
(2)连接AD,结合AC=AB、DC=DB即可证出△ABD≌△ACD(SSS),由此即可得出∠BDA=∠CDA=60°,再根据∠EDG=60°即可得出∠CDE=∠ADG,∠ADE=∠BDG,由(1)可知△CDE≌△BDF,进而得知∠CDE=∠BDF,根据角的计算即可得出∠EDG=∠FDG,结合DE=DF即可证出△DEG≌△DFG(SAS),即得出EG=FG,由相等的边与边之间的关系即可证出CE+BG=EG.
(1)∵∠CAB+∠C+∠CDB+∠ABD=360°,∠CAB=60°,∠CDB=120°,
∴∠C+∠ABD=360°-60°-120°=180°,
又∵∠DBF+∠ABD=180°,
∴∠C=∠DBF,
在△CDE和△BDF中,
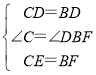 ,
,
∴△CDE≌△BDF(SAS),
∴DE=DF;
(2)如图,连接AD,
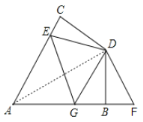
猜想CE、EG、BG之间的数量关系为:CE+BG=EG.
证明:在△ABD和△ACD中,
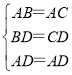 ,
,
∴△ABD≌△ACD(SSS),
∴∠BDA=∠CDA=![]() ∠CDB=
∠CDB=![]() ,
,
又∵∠EDG=60°,
∴∠CDE=∠ADG,∠ADE=∠BDG,
由(1),可得△CDE≌△BDF,
∴∠CDE=∠BDF,
∴∠BDG+∠BDF=60°,
即∠FDG=60°,
∴∠EDG=∠FDG,
在△DEG和△DFG中,
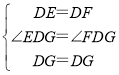 ,
,
∴△DEG≌△DFG,
∴EG=FG,
又∵CE=BF,FG=BF+BG,
∴CE+BG=EG.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
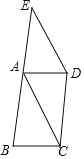
【题目】如图,已知四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接DE,AC
(1)求证:四边形ACDE为平行四边形;
(2)连接CE交AD于点O,若AC=AB=3,cosB=![]() ,求线段CE的长.
,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
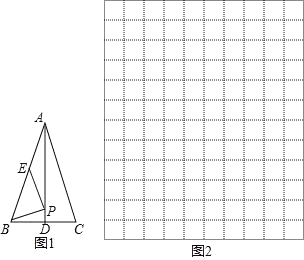
【题目】如图 1,在等腰△ABC 中,AB=AC,点 D,E 分别为 BC,AB 的中点,连接 AD.在线段 AD 上任取一点 P,连接 PB,PE.若 BC=4,AD=6,设 PD=x(当点 P 与点 D 重合时,x 的值为 0),PB+PE=y.
小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
说明:补全表格时,相关数值保留一位小数.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)
≈2.236)
(2)建立平面直角坐标系(图 2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)求函数 y 的最小值(保留一位小数),此时点 P 在图 1 中的什么位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD,添加下列条件不能使四边形ABCD成为平行四边形的是( )
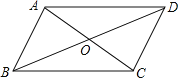
A.AB=CDB.OB=OD
C.∠BCD+∠ADC=180°D.AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=-x2+5x+n经过点A(1,0),与x轴交于点C,与y轴交于点B,顶点为D.
(1)求n的值和D点坐标;
(2)求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com