
【题目】(1)如图1.在△ABC中,∠B=60°,∠DAC和∠ACE的角平分线交于点O,则∠O= °,
(2)如图2,若∠B=α,其他条件与(1)相同,请用含α的代数式表示∠O的大小;
(3)如图3,若∠B=α,![]() ,则∠P= (用含α的代数式表示).
,则∠P= (用含α的代数式表示).

【答案】(1)∠O=60°;(2)90°-![]() ;(3)
;(3)![]()
【解析】
(1)由题意利用角平分线的性质和三角形内角和为180°进行分析求解;
(2)根据题意设∠BAC=β,∠ACB=γ,则α+β+γ=180°,利用角平分线性质和外角定义找等量关系,用含α的代数式表示∠O的大小;
(3)利用(2)的条件可知n=2时,∠P=![]() ,再将2替换成n即可分析求解.
,再将2替换成n即可分析求解.
解:(1)因为∠DAC和∠ACE的角平分线交于点O,且∠B=60°,
所以![]() ,
,
有∠O=![]() 60°.
60°.
(2)设∠BAC=β,∠ACB=γ,则α+β+γ=180°
∵∠ACE是△ABC的外角,
∴∠ACE=∠B+∠BAC=α+β
∵CO平分∠ACE
![]()
同理可得:![]()
∵∠O+∠ACO+∠CAO=180°,
∴![]()
![]()
![]() ;
;
(3)∵∠B=α,![]() ,
,
由(2)可知n=2时,有∠P=![]() =
=![]() ,将2替换成n即可,
,将2替换成n即可,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在; ④使得M=1的x值是![]() 或
或![]() .
.
其中正确的是( )

A.①② B.①④ C.②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
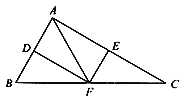
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,-1),B(2,3),点P为x轴上一点,当|PA-PB|的值最大时,点P的坐标为( )
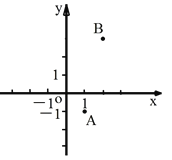
A.(-1,0)B.(![]() ,0)C.(
,0)C.(![]() ,0)D.(1,0)
,0)D.(1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校团委决定对甲、乙、丙三位候选人进行民主投票、笔试、面试考核,从中推选一名担任学生会主席.已知参加民主投票的学生为200名,每人当且仅当推荐一名候选人,民主投票结果如下扇形统计图所示,笔试和面试的成绩如下统计表所示.
甲 | 乙 | 丙 | |
笔试 | 78 | 80 | 85 |
面试 | 92 | 75 | 70 |
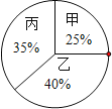
(1)甲、乙、丙的得票数依次是______、______、______;
(2)若民主投票得一票记1分,学校将民主投票、笔试、面试三项得分按3:4:3的比例确定三名候选人的考核成绩,成绩最高当选,请通过计算确定谁当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,直线l1:y=kx+4与y轴交于点A,与x轴交于点B.
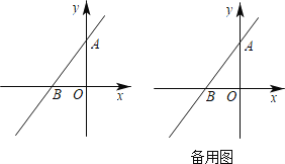
(1)请直接写出点A的坐标:______;
(2)点P为线段AB上一点,且点P的横坐标为m,现将点P向左平移3个单位,再向下平移4个单位,得点P′在射线AB上.
①求k的值;
②若点M在y轴上,平面内有一点N,使四边形AMBN是菱形,请求出点N的坐标;
③将直线l1绕着点A顺时针旋转45°至直线l2,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC,垂足为D,∠ACB的平分线交AD于点E,则AE的长为( )

A.![]() B.4
B.4![]() C.
C.![]()
![]() D.6
D.6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com