
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
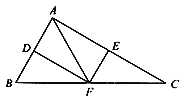
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
【答案】(1)证明见解析 (2)![]()
【解析】
(1)连接DE.根据三角形的中位线的性质即可得到结论;
(2)根据矩形的性质得到∠BAC=∠FEC=90°,解直角三角形即可得到结论.
(1)连接DE,
∵E、F分别是AC,BC中点
∴EF//AB,EF=![]() AB
AB
∵点D是AB中点
∴AD=![]() AB,AD=EF
AB,AD=EF
∴四边形ADFE为平行四边形
∵点D、E分别为AB、AC中点
∴DE=![]() BC,
BC,
∵BC=2AF
∴DE=AF
∴四边形ADEF为矩形.
(2)∵四边形ADFE是矩形,
∴∠BAC=∠FEC=90°,
∵AF=2,F为BC中点,
∴BC=4,CF=2,
∵∠C=30°
∴AC=![]() ,CE=
,CE=![]() ,EF=1,
,EF=1,
∴AE=![]()
∴矩形ADEF的周长为![]() ;
;


科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)当顶点坐标为![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(2)当![]() 时,
时,![]() ,
,![]() 是抛物线图象上的两点,且
是抛物线图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若抛物线上的点![]() ,满足
,满足![]() 时,
时,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西宁教育局在局属各初中学校设立“自主学习日”.规定每周三学校不得以任何形式布置家庭作业,为了解各学校的落实情况,从七、八年级学生中随机抽取了部分学生的反馈表.针对以下六个项目(每人只能选一项):![]() .课外阅读;
.课外阅读;![]() .家务劳动;
.家务劳动;![]() .体育锻炼;
.体育锻炼;![]() .学科学习;
.学科学习;![]() .社会实践;
.社会实践;![]() .其他项目进行调查.根据调查结果绘制了如下尚不完整的统计图,请你根据统计图解答下列问题:
.其他项目进行调查.根据调查结果绘制了如下尚不完整的统计图,请你根据统计图解答下列问题:
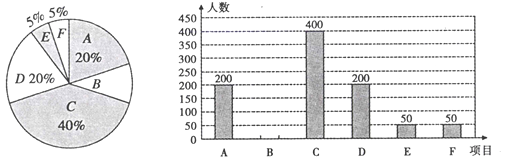
(1)此次抽查的样本容量为____________,请补全条形统计图;
(2)全市约有4万名在校初中学生,试估计全市学生中选择体育锻炼的人数约有多少人?
(3)七年级(1)班从选择社会实践的2名女生和1名男生中选派2名参加校级社会实践活动.请你用树状图或列表法求出恰好选到1男1女的概率是多少?并列举出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
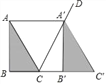
【题目】如图,将△ABC沿着射线BC方向平移至△A′B′C′,使点A′落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A′的形状,并说明理由;
(2)在△ABC中,∠B=90°,AB=8,cos∠BAC=![]() ,求CB′的长.
,求CB′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
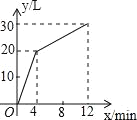
【题目】一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)每分钟进水、出水各多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com