
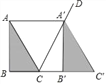
【题目】如图,将△ABC沿着射线BC方向平移至△A′B′C′,使点A′落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A′的形状,并说明理由;
(2)在△ABC中,∠B=90°,AB=8,cos∠BAC=![]() ,求CB′的长.
,求CB′的长.
【答案】(1)见解析;(2)4.
【解析】分析:
(1)由平移的性质结合平行四边形的判定方法易得四边形ACC′A′是平行四边形,由AA′∥CC′结合CD平分∠ACC′证得∠ACA'=∠AA'C,可得AA'=AC,从而可得平行四边形ACC′A′是菱形;
(2)在Rt△ABC中由已知条件易得AC=10,BC=6,结合平移的性质和四边形ACC′A′是菱形即可求得CB′的长度.
详解:
(1)四边形ACC′A′是菱形,理由如下:
由平移的性质可得:AA'=CC',且AA'∥CC'
∴四边形ACC′A′是平行四边形,
∵AA'∥CC',
∴∠AA'C=∠A'CB',
∵CD平分∠ACB',
∴∠ACA'=∠A'CB',
∴∠ACA'=∠AA'C,
∴AA'=AC,
∴平行四边形ACC′A′是菱形;
(2)在Rt△ABC中,∠B=90°,AB=8,
∴cos∠BAC=![]() ,
,
∴AC=10,
∴BC=![]()
由平移的性质可得:BC=B'C'=6,
由(1)得四边形ACC′A′是菱形,
∴AC=CC'=10,
∴CB'=CC'﹣B'C'=10﹣6=4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 6 | 5 | 2200元 |
第二周 | 4 | 10 | 3200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
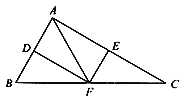
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1=22-02,a2=32-12,…,an=(n+1)2-(n-1)2(n为大于1的整数)
(1)计算a15的值;
(2)通过拼图你发现前三个图形的面积之和与第四个正方形的面积之间有什么关系:
__________________________________(用含a、b的式子表示);

(3)根据(2)中结论,探究an=(n+1)2-(n-1)2是否为4的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面各图,寻找对顶角(不含平角)
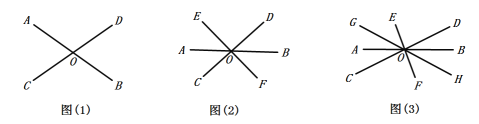
(1)如图(1),图中共有________对不同的对顶角.
(2)如图(2),图中共有________对不同的对顶角.
(3)如图(3),图中共有________对不同的对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有![]()
![]() 条直线相交于一点,则可形成________对不同的对顶角.
条直线相交于一点,则可形成________对不同的对顶角.
(5)计算2013条直线相交于一点,则可形成________对不同的对顶角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=![]() cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒![]() cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线y=![]() x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
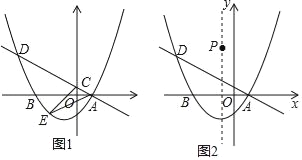
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣![]() 与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
(1)求抛物线的函数表达式;
(2)若点D在第二象限且满足CD=5AC,求此时直线1的解析式;在此条件下,点E为直线1下方抛物线上的一点,求△ACE面积的最大值,并求出此时点E的坐标;
(3)如图,设P在抛物线的对称轴上,且在第二象限,到x轴的距离为4,点Q在抛物线上,若以点A,D,P,Q为顶点的四边形能否成为平行四边形?若能,请直接写出点Q的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
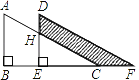
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com