
【题目】已知抛物线![]() .
.
(1)当顶点坐标为![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(2)当![]() 时,
时,![]() ,
,![]() 是抛物线图象上的两点,且
是抛物线图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若抛物线上的点![]() ,满足
,满足![]() 时,
时,![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]()
【解析】分析:(1)利用抛物线的顶点坐标公式即可得出结论;
(2)先确定出抛物线对称轴x=﹣1,进而得出点Q的坐标,即可得出结论;
(3)分三种情况利用抛物线的增减性建立方程组即可得出结论.
详解:(1)由已知得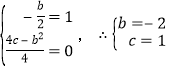 ,
,
∴抛物线的解析式为 y=x2﹣2x+1;
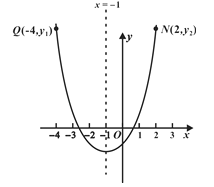
(2)当b=2时,y=x2+2x+c, ∴对称轴直线x=﹣1.
由图取抛物线上点Q,使Q与N关于对称轴x=﹣1对称,由N(2,y2)得Q(﹣4,y2).
又∵M(m,y1)在抛物线图象上的点,且y1>y2,由函数增减性得:m<﹣4或m>2;
(3)分三种情况:
①当﹣![]() <﹣1,即b>2时,函数值y随x的增大而增大,依题意有:
<﹣1,即b>2时,函数值y随x的增大而增大,依题意有:![]()
②当﹣1≤﹣![]() ≤1,即﹣2≤b≤2时,x=﹣
≤1,即﹣2≤b≤2时,x=﹣![]() 时,函数值y取最小值,分两种情况讨论:
时,函数值y取最小值,分两种情况讨论:
(ⅰ)若0≤﹣![]() ≤1,即﹣2≤b≤0时,依题意有:
≤1,即﹣2≤b≤0时,依题意有:
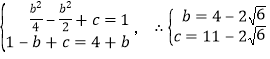 或
或![]() (舍去)
(舍去)
(ⅱ)若﹣1≤﹣![]() ≤0,即0≤b≤2时,依题意有
≤0,即0≤b≤2时,依题意有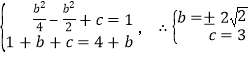 (舍去)
(舍去)
③当﹣![]() >1,即b<﹣
>1,即b<﹣![]() (舍去)
(舍去)
综上所述:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,反比例函数y=![]() 图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
(1)求k的值和点E的坐标;
(2)直接写出不等式![]() -n>mx的解集;
-n>mx的解集;
(3)点Q为x轴上一点,点P为反比例函数y=![]() 图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x、y是任意两个有理数,规定x与y之间的一种运算“⊕”为:
x⊕y=![]()
(1)试求1⊕(-1)的值;
(2)试判断该运算“⊕”是否具有交换律,说明你的理由;
(3)若2⊕x=0,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 6 | 5 | 2200元 |
第二周 | 4 | 10 | 3200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 观察下列三行数:
2,4,8,16,32,![]()
![]() ,1,2,4,8,
,1,2,4,8,![]()
1,5,7,17,31,![]()
如图,第一行数的第n(n为正整数)个数![]() 用来表示,第二行数的第n个数用
用来表示,第二行数的第n个数用![]() 来表示,第三行数的第n个数用
来表示,第三行数的第n个数用![]() 来表示
来表示
(1)根据你发现的规律,请用含n的代数式表示数![]() ,
,![]() ,
,![]() 的值
的值![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
(2)取每行的第6个数,计算这三个数的和
(3)若![]() 记为x,求
记为x,求![]() (结果用含x的式子表示并化简)
(结果用含x的式子表示并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
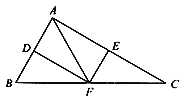
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1=22-02,a2=32-12,…,an=(n+1)2-(n-1)2(n为大于1的整数)
(1)计算a15的值;
(2)通过拼图你发现前三个图形的面积之和与第四个正方形的面积之间有什么关系:
__________________________________(用含a、b的式子表示);

(3)根据(2)中结论,探究an=(n+1)2-(n-1)2是否为4的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=![]() cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒![]() cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线y=![]() x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们环保意识的增强,“低碳出行”越来越为人们所倡导。小李要从家乡到宁波工作,若乘飞机需要3小时,乘汽车需要9小时。这两种交通工具每小时排放的二氧化碳总量为80千克,已知飞机每小时二氧化碳的排放量比汽车多46千克,若小李乘汽车来宁波,那么他此行与乘飞机相比将减少二氧化碳排放量多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com