
【题目】如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,反比例函数y=![]() 图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
(1)求k的值和点E的坐标;
(2)直接写出不等式![]() -n>mx的解集;
-n>mx的解集;
(3)点Q为x轴上一点,点P为反比例函数y=![]() 图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

【答案】(1)k= 3,E(2,![]() );(2)0<x<1或x>2;(3)存在;使得以P、Q、D、E为顶点的四边形为平行四边形的P点的坐标为(-2,-
);(2)0<x<1或x>2;(3)存在;使得以P、Q、D、E为顶点的四边形为平行四边形的P点的坐标为(-2,-![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)将D的坐标,代入反比例函数的解析式可求得k的值,然后求得点E的纵坐标,然后将点E的横坐标代入反比例函数的解析式可求得点E的纵坐标;
(2)不等式![]() -n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围;
-n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围;
(3)分为ED为平行四边形的一边和DE为平行四边形的对角线两种情况列方程求解即可.
解:(1)k=xy=1×3=3,
∴反比例函数的解析式为y=![]() .
.
∵D是AB的中点,D(1,3),
∴E点的横坐标为2.
∴yE=![]() .
.
∴E(2,![]() ).
).
(2)∵不等式![]() -n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围,
-n>mx的解集为反比例函数图象位于直线上方部分自变量x的取值范围,
∴不等式的解集为0<x<1或x>2.
(3)存在;
∵D(1,3),E(2,![]() ),以P、Q、D、E为顶点的四边形为平行四边形,
),以P、Q、D、E为顶点的四边形为平行四边形,
当DE是平行四边形的边时,则PQ∥DE,且PQ=DE,
∴Q的纵坐标为0,
∴P的纵坐标为±![]() ,
,
令y=![]() ,则
,则![]() =
=![]() ,解得x=2(舍去),
,解得x=2(舍去),
令y=-![]() ,则-
,则-![]() =
=![]() ,解得x=-2,
,解得x=-2,
∴P点的坐标为(-2,-![]() );
);
当DE是平行四边形的对角线时,
∵D(1,3),E(2,![]() ),
),
∴DE的中点为(![]() ,
,![]() ),
),
设P(a,![]() )、Q(x,0),
)、Q(x,0),
∴![]() ÷2=
÷2=![]() ,
,![]() =
=![]() ,解得:a=
,解得:a=![]() ,x=
,x=![]() .
.
∴P(![]() ,
,![]() ),
),
故使得以P、Q、D、E为顶点的四边形为平行四边形的P点的坐标为(-2,-![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的重量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准重量的差值(单位:g) | ﹣5 | ﹣2 | 0 | 1 | 3 | 6 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)计算这批样品的平均重量,判断它比标准重量重还是轻多少?
(2)若标准重量为450克,则这批样品的总重量是多少?
(3)若这种食品的合格标准为450±5克,则这批样品的合格率为 (直接填写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想利用太阳光测量楼高,发现对面墙上有这栋楼的影子,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠且高度恰好相同.此时测得墙上影子高![]() ,
,![]() ,
,![]() (点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.
(点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
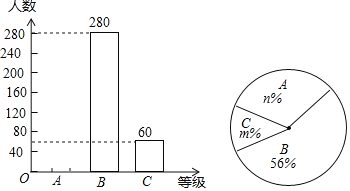
(1)这次调查的市民人数为_____人;
(2)补全条形统计图;
(3)计算扇形统计图中等级C对应的圆心角的度数;
(4)若该市约有市民1000000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如下图所示:

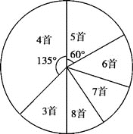
大赛结束后一个月,再次调查这部分学生“一周诗词诵背数量”,绘制成统计表:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人 数 | 10 | 10 | 15 | m | 25 | 20 |
请根据调查的信息
(1)本次调查抽取了多少名学生?
(2)补全条形统计图,在扇形统计图中,“6首”的圆心角为 度;
(3)表格中m的值为 ;
(4)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在二次函数y=ax2+bx+c的图象中,你认为其中正确的是( )
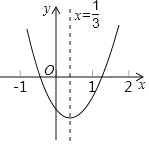
A. a>0 B. c>0
C. b2﹣4ac<0 D. 一元二次方程ax2+bx+c=0有两个相等实根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)当顶点坐标为![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(2)当![]() 时,
时,![]() ,
,![]() 是抛物线图象上的两点,且
是抛物线图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若抛物线上的点![]() ,满足
,满足![]() 时,
时,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com