
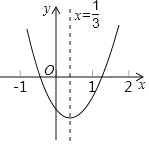
【题目】如图,在二次函数y=ax2+bx+c的图象中,你认为其中正确的是( )
A. a>0 B. c>0
C. b2﹣4ac<0 D. 一元二次方程ax2+bx+c=0有两个相等实根
【答案】A
【解析】
本题考查了二次函数图象与系数之间的关系,对于二次函数y=ax2+bx+c(a≠0)来说,
①二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口.
②一次项系数b和二次项系数a共同决定对称轴的位置.当a与b同号时(即ab>0),对称轴在y轴左侧; 当a与b异号时(即ab<0),对称轴在y轴右侧.(简称:左同右异)
③常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
根据这些内容依次判定即可.
解:∵抛物线开口向上,
∴a>0(则A正确),
∵抛物线与y轴的交点在x轴的下方,
∴c<0(则B错误),
∵抛物线与x轴有两个交点,
∴b2-4ac>0(则C错误),
∴一元二次方程ax2+bx+c=0有两个不相等实根(则D错误),
综上可知A正确,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
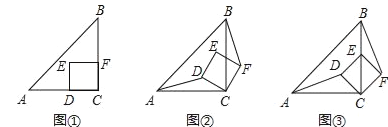
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D、F分别在边AC、BC上,易证:AD=BF(不需要证明);
探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD、BF,其他条件不变,如图②,求证:AD=BF;
应用:若α=45°,CD=![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
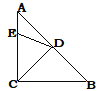
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,反比例函数y=![]() 图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
图象经过AB的中点D(1,3),且与BC交于点E,设直线DE的解析式为y=mx+n.
(1)求k的值和点E的坐标;
(2)直接写出不等式![]() -n>mx的解集;
-n>mx的解集;
(3)点Q为x轴上一点,点P为反比例函数y=![]() 图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
图象上一点,是否存在点P、Q,使得以P、Q、D、E为顶点的四边形为平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点之间的距离等于相应两数差的绝对值,即:点A、B表示的数分别为a、b,这两点之间的距离为AB=![]() ,如:表示数1与5的两点之间的距离可表示为
,如:表示数1与5的两点之间的距离可表示为![]() ,表示数-2与3的两点之间的距离可表示为
,表示数-2与3的两点之间的距离可表示为![]() .
.
(1)数轴上表示2和7的两点之间的距离是 ,数轴上表示3和-6的两点之间的距离是 ;
(2)数轴上表示x和-2的两点M和N之间的距离是 ,如果![]() ,则x为 ;
,则x为 ;
(3)当式子:![]() 取最小值时,x的值为 ,最小值为 .
取最小值时,x的值为 ,最小值为 .
(借助数轴,画出图形,写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了解居民对居住环境的满意度情况(满意度分为四个等级:![]() 、非常满意:
、非常满意:![]() 、满意;
、满意;![]() 、基本满息;
、基本满息;![]() 、不满意),在某小区随机抽样调查了若干户居民,并根据调查数据绘制成下面两个不完整的统计图.
、不满意),在某小区随机抽样调查了若干户居民,并根据调查数据绘制成下面两个不完整的统计图.

请你结合图中提供的信息解答下列问题.
(1)这次被调查的居民共有______户,并将条形统计图补充完整.
(2)请计算扇形统计图中![]() 所在扇形的圆心角度数.
所在扇形的圆心角度数.
(3)若该小区有2500户居民,请你估计这个小区大约有多少户居民对居住环境的满意度是“非常满意”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x、y是任意两个有理数,规定x与y之间的一种运算“⊕”为:
x⊕y=![]()
(1)试求1⊕(-1)的值;
(2)试判断该运算“⊕”是否具有交换律,说明你的理由;
(3)若2⊕x=0,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1=22-02,a2=32-12,…,an=(n+1)2-(n-1)2(n为大于1的整数)
(1)计算a15的值;
(2)通过拼图你发现前三个图形的面积之和与第四个正方形的面积之间有什么关系:
__________________________________(用含a、b的式子表示);

(3)根据(2)中结论,探究an=(n+1)2-(n-1)2是否为4的倍数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com