
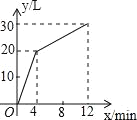
【题目】一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)每分钟进水、出水各多少升?
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
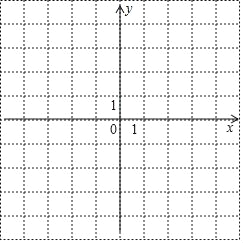
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
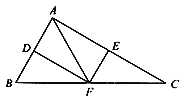
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面各图,寻找对顶角(不含平角)
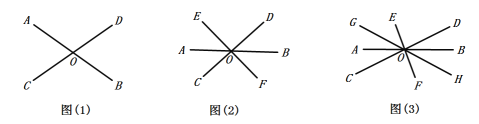
(1)如图(1),图中共有________对不同的对顶角.
(2)如图(2),图中共有________对不同的对顶角.
(3)如图(3),图中共有________对不同的对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有![]()
![]() 条直线相交于一点,则可形成________对不同的对顶角.
条直线相交于一点,则可形成________对不同的对顶角.
(5)计算2013条直线相交于一点,则可形成________对不同的对顶角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=![]() cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒![]() cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线y=![]() x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各题计算正确的是 ( )
A. (ab﹣1)·(﹣4ab2)=﹣4a2b3﹣4ab2 B. (3x2+xy﹣y2)·3x2=9x4+3x3y﹣y2
C. (﹣3a)·(a2﹣2a+1)=﹣3a3+6a2 D. (﹣2x)·(3x2﹣4x﹣2)=﹣6x3+8x2+4x
查看答案和解析>>
科目:初中数学 来源: 题型:
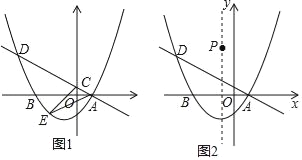
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣![]() 与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
(1)求抛物线的函数表达式;
(2)若点D在第二象限且满足CD=5AC,求此时直线1的解析式;在此条件下,点E为直线1下方抛物线上的一点,求△ACE面积的最大值,并求出此时点E的坐标;
(3)如图,设P在抛物线的对称轴上,且在第二象限,到x轴的距离为4,点Q在抛物线上,若以点A,D,P,Q为顶点的四边形能否成为平行四边形?若能,请直接写出点Q的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
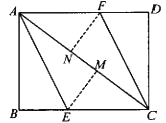
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处。
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com