
【题目】如图,在平面直角坐标系中,O为坐标原点,直线l1:y=kx+4与y轴交于点A,与x轴交于点B.
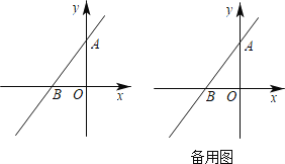
(1)请直接写出点A的坐标:______;
(2)点P为线段AB上一点,且点P的横坐标为m,现将点P向左平移3个单位,再向下平移4个单位,得点P′在射线AB上.
①求k的值;
②若点M在y轴上,平面内有一点N,使四边形AMBN是菱形,请求出点N的坐标;
③将直线l1绕着点A顺时针旋转45°至直线l2,求直线l2的解析式.
【答案】(1)(0,4);(2)①k=![]() ;②N(-3,
;②N(-3,![]() );③直线l2的解析式为y=
);③直线l2的解析式为y=![]() x+4.
x+4.
【解析】
(1)令![]() ,求出相应的y值,即可得到A的坐标;
,求出相应的y值,即可得到A的坐标;
(2)①先设出P的坐标,然后通过点的平移规律得出平移后![]() 的坐标,然后将
的坐标,然后将![]() 代入
代入![]() 中即可求出k的值;
中即可求出k的值;
②作AB的中垂线与y轴交于M点,连结BM,分别作AM,BM的平行线,相交于点N,则四边形AMBN是菱形, 设M(0,t),然后利用勾股定理求出t的值,从而求出OM的长度,然后利用BN=AM求出BN的长度,即可得到N的坐标;
③先根据题意画出图形,过点B作BC⊥l1,交l2于点C,过点C作CD⊥x轴于D,利用等腰三角形的性质和AAS证明△AOB≌△BDC,得出AO=BD,OB=DC,进一步求出点C的坐标,然后利用待定系数法即可求出直线l2的解析式.
(1)∵y=kx+4与y轴交于点A,
令![]() ,
,![]() ,
,
∴A(0,4).
(2)①由题意得:P(m,km+4),
∵将点P向左平移3个单位,再向下平移4个单位,得点P′,
∴P′(m-3,km),
∵P′(m-3,km)在射线AB上,
∴k(m-3)+4=km,
解得:k=![]() .
.
②如图,作AB的中垂线与y轴交于M点,连结BM,过点B作AM的平行线,过点A作BM的平行线,两平行线相交于点N,则四边形AMBN是菱形.
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() .
.
设M(0,t),则AM=BM=4-t,

在Rt△BOM中,OB2+OM2=BM2,
即32+t2=(4-t)2,
解得:t=![]() ,
,
∴M(0,![]() ),
),
∴OM=![]() ,BN=AM=4-
,BN=AM=4-![]() =
=![]() ,
,
∴N(-3,![]() ).
).
③如图,过点B作BC⊥l1,交l2于点C,过点C作CD⊥x轴于D.则∠ABC=∠BDC=90°,
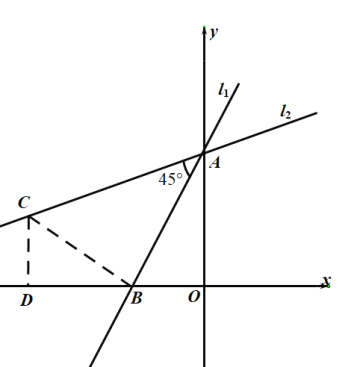
∵∠BAC=45°,
∴△ABC是等腰直角三角形,
∴AB=BC,∠ABO+∠CBD=90°,
又∵∠ABO+∠BAO=90°,
∴∠BAO=∠CBD,
在![]() 和
和![]() 中,
中,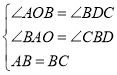
∴△AOB≌△BDC(AAS),
∴AO=BD=4,OB=DC=3,
∴OD=OB+BD=3+4=7,
∴C(-7,3),
设直线 l2的解析式为:y=ax+4,
则-7a+4=3,
解得:a=![]() .
.
∴直线 l2的解析式为:y=![]() x+4.
x+4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: ①a+b+c<0;②a–b+c<0;③b+2a<0;④abc>0,其中正确的是 (填写正确的序号)。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1.在△ABC中,∠B=60°,∠DAC和∠ACE的角平分线交于点O,则∠O= °,
(2)如图2,若∠B=α,其他条件与(1)相同,请用含α的代数式表示∠O的大小;
(3)如图3,若∠B=α,![]() ,则∠P= (用含α的代数式表示).
,则∠P= (用含α的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
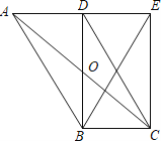
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:在平面直角坐标系内,O为坐标原点,线段AB两端点在坐标轴上且点A(﹣4,0),点B(0,3),将AB向右平移4个单位长度至OC的位置
(1)直接写出点C的坐标 ;
(2)如图2,过点C作CD⊥x轴于点D,在x轴正半轴有一点E(1,0),过点E作x轴的垂线,在垂线上有一动点P,直接写出:①点D的坐标 ; ②三角形PCD的面积为 ;
(3)如图3,在(2)的条件下,连接AC,当△ACP的面积为![]() 时,直接写出点P的坐标 .
时,直接写出点P的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.
(1)让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?
(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com