练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知x＝，y＝

    （1）求x2+xy+y2．

    （2）若x的小数部分为a，y的整数部分为b，求ax+by的平方根．

    【答案】（1）19；（2）±1．

    【解析】

    （1）先分母有理化求出x、y的值，再求出x+y和xy的值，最后根据完全平方公式进行变形，代入求出即可；

    （2）先求出x、y的范围，再求出a、b的值，最后代入求出即可．

    解：（1）x＝＝＝+2，y＝＝﹣2，

    x+y＝（+2）+（﹣2）＝2，xy＝（+2）×（﹣2）＝5﹣4＝1，

    x2+xy+y2＝（x+y）2﹣xy＝（2）2﹣1＝19；

    （2）∵2＜＜3，

    ∴4＜+2＜5，0＜﹣2＜1，

    ∴a＝+2﹣4＝﹣2，y＝0，

    ∴ax+by＝（﹣2）（+2）+（﹣2）×0＝5﹣4＝1，

    ∴ax+by的平方根是±＝±1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】《九章算术》是我国古代数学名著，书中有下列问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为“今有直角三角形，勾(短直角边)长为5步，股(长直角边)长为12步，问该直角三角形能容纳的正方形边长最大是多少步？”该问题的答案是________步．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A，B，C三点在⊙O上，直径BD平分∠ABC，过点D作DE∥AB交弦BC于点E，在BC的延长线上取一点F，使得EFDE．

    （1）求证：DF是⊙O的切线；

    （2）连接AF交DE于点M，若 AD4，DE5，求DM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y1=﹣2x2+2，直线y2=2x+2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．下列判断：

    ①当x＞0时，y1＞y2； ②当x＜0时，x值越大，M值越小；

    ③使得M大于2的x值不存在； ④使得M=1的x值是或．

    其中正确的是（　　）

    　　A．①②　　B．①④　　C．②③　　D．③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线（a ≠ 0）满足条件：（1）；（2）；

    （3）与x轴有两个交点，且两交点间的距离小于2．以下有四个结论：①；

    ②；③；④，其中所有正确结论的序号是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知BD是△ABC的角平分线，ED⊥BC，∠BAC=90°，∠C=30°．

    （1）求证：CE=BE；

    （2）若AD=3，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴交于A（－1，0），B（3，0）两点，与轴交于点C，顶点为D，下列结论正确的是（ ）

    A. abc＜0 B. 3a+c=0 C. 4a-2b+c＜0 D. 方程ax2+bx+c=-2（a≠0）有两个不相等的实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D、E、F分别是边AB、AC、BC的中点，且BC=2AF。

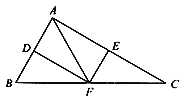
    （1）求证：四边形ADEF为矩形；

    （2）若∠C=30°、AF=2，写出矩形ADEF的周长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，直线l1：y=kx+4与y轴交于点A，与x轴交于点B．

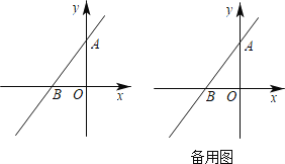
    （1）请直接写出点A的坐标：______；

    （2）点P为线段AB上一点，且点P的横坐标为m，现将点P向左平移3个单位，再向下平移4个单位，得点P′在射线AB上．

    ①求k的值；

    ②若点M在y轴上，平面内有一点N，使四边形AMBN是菱形，请求出点N的坐标；

    ③将直线l1绕着点A顺时针旋转45°至直线l2，求直线l2的解析式．

    查看答案和解析>>

    同步练习册答案