
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.

【答案】![]()
【解析】
如图1,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论;如图2,同理可得正方形的边长,比较可得最大值.
解:如图1,

∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12-x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
x=![]() ,
,
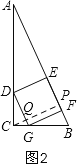
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,
S△ABC=![]() ACBC=
ACBC=![]() ABCP,
ABCP,
12×5=13CP,
CP=![]() ,
,
同理得:△CDG∽△CAB,
∴![]() =
=![]() ,
,
∴![]() =
=![]()
![]() ,
,
x=![]() <
<![]() ,
,
∴该直角三角形能容纳的正方形边长最大是![]() (步),
(步),
故答案为:![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
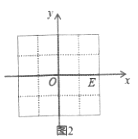
【题目】问题情境:
在平面直角坐标系![]() 中有不重合的两点
中有不重合的两点![]() 和点
和点![]() ,小明在学习中发现,若
,小明在学习中发现,若![]() ,则
,则![]() 轴,且线段
轴,且线段![]() 的长度为
的长度为![]() ;若
;若![]() ,则
,则![]() 轴,且线段
轴,且线段![]() 的长度为
的长度为![]() ;
;
(应用):
(1)若点![]() 、
、![]() ,则
,则![]() 轴,
轴,![]() 的长度为__________.
的长度为__________.
(2)若点![]() ,且
,且![]() 轴,且
轴,且![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
(拓展):
我们规定:平面直角坐标系中任意不重合的两点![]() ,
,![]() 之间的折线距离为
之间的折线距离为![]() ;例如:图1中,点
;例如:图1中,点![]() 与点
与点![]() 之间的折线距离为
之间的折线距离为![]() .
.
解决下列问题:
(1)如图1,已知![]() ,若
,若![]() ,则
,则![]() __________;
__________;
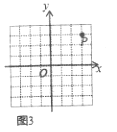
(2)如图2,已知![]() ,
,![]() ,若
,若![]() ,则
,则![]() __________.
__________.
(3)如图3,已知![]() 的,点
的,点![]() 在
在![]() 轴上,且三角形
轴上,且三角形![]() 的面积为3,则
的面积为3,则![]() __________.
__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
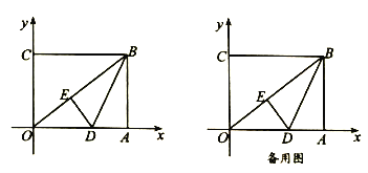
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
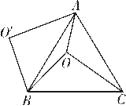
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;&
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AOBO′的面积为6+3![]() ;
;
⑤S△AOC+S△AOB=6+![]() .
.
其中正确的结论是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1) 求y与x的函数关系式;
(2) 根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的![]() ,那么他的月收入最高能达到多少元?
,那么他的月收入最高能达到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
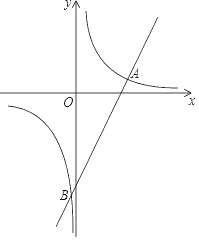
【题目】如图,一次函数y=mx+b的图象与反比例函数y=![]() 的图象交于A(3,1),B(﹣
的图象交于A(3,1),B(﹣![]() ,n)两点.
,n)两点.
(1)求该反比例函数的解析式;
(2)求n的值及该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
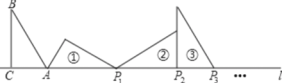
【题目】如图,Rt△ABC中,∠ACB=90°,AC=1,∠B=30°,且AC边在直线l上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时![]() ;……,按此规律继续旋转,直至得到点
;……,按此规律继续旋转,直至得到点![]() 为止,则
为止,则![]() =___________.
=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3过点A(-1,0),B(3,0),点M,N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.
(1)求抛物线的表达式;
(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;
(3)若∠DMN=90°,MD=MN,直接写出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com