
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;&
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AOBO′的面积为6+3![]() ;
;
⑤S△AOC+S△AOB=6+![]() .
.
其中正确的结论是_______________.
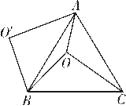
【答案】①②③⑤.
【解析】
证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;
由△OBO′是等边三角形,可知结论②正确;
在△AOO′中,三边长为3,4,5,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=6+4![]() ,故结论④错误;
,故结论④错误;
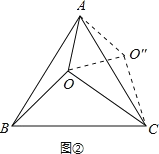
如图②,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O′′点.利用旋转变换构造等边三角形与直角三角形,将S△AOC+S△AOB转化为S△COO″+S△AOO″,计算可得结论⑤正确.

由题意可知,∠1+∠2=∠3+∠2=60°,
∴∠1=∠3,
又∵OB=O′B,AB=BC,
在△BO′A和△BOC中,
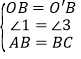 ,
,
∴△BO′A≌△BOC(SAS),
又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,
故结论①正确;
如图①,连接OO′,
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=4.
故结论②正确;
∵△BO′A≌△BOC,∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=![]() ×3×4+
×3×4+![]() ×42=6+4
×42=6+4![]() ,
,
故结论④错误;
如图②所示,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O′′点.
易知△AOO′′是边长为3的等边三角形,△COO′′是边长为3、4、5的直角三角形,
则S△AOC+S△AOB=S四边形AOCO'=S△COO'+S△AOO'=![]() ×3×4+
×3×4+![]() ×32=6+
×32=6+![]() ,
,
故结论⑤正确.
综上所述,正确的结论为:①②③⑤.
故答案为:①②③⑤.


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC交O于点D,E是弧CD的中点,连接AE交BC于点F,∠ABC=2∠EAC.
(1)求证:AB是⊙O的切线;
(2)若 tanB=![]() ,BD=6,求CF的长.
,BD=6,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一般地,数轴上表示数m和数n的两点之间的距离等于![]() .如果表示数a和
.如果表示数a和![]() 的两点之间的距离是5,那么
的两点之间的距离是5,那么![]() __________;
__________;
(2)若数轴上表示数a的点位于![]() 与6之间,求
与6之间,求![]() 的值;
的值;
(3)当a取何值时,![]() 的值最小,最小值是多少?请说明理由.
的值最小,最小值是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在; ④使得M=1的x值是![]() 或
或![]() .
.
其中正确的是( )

A.①② B.①④ C.②③ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com