
����Ŀ����ͼ1����![]() �У�
��![]() ��E��
��E��![]() ��D��AE�ϵ�һ�㣬��
��D��AE�ϵ�һ�㣬��![]() ������BD��CD��
������BD��CD��

![]() ���ж�BD��AC��λ�ù�ϵ��������ϵ����˵�����ɣ�
���ж�BD��AC��λ�ù�ϵ��������ϵ����˵�����ɣ�
![]() ��ͼ2������
��ͼ2������![]() �Ƶ�E��תһ���ĽǶȺ����ж�BD��AC��λ�ù�ϵ��������ϵ�Ƿ����仯����˵�����ɣ�
�Ƶ�E��תһ���ĽǶȺ����ж�BD��AC��λ�ù�ϵ��������ϵ�Ƿ����仯����˵�����ɣ�
![]() ��ͼ3������
��ͼ3������![]() �еĵ���ֱ�������ζ����ɵȱ������Σ������������䣮
�еĵ���ֱ�������ζ����ɵȱ������Σ������������䣮
![]() �Բ���BD��AC��������ϵ����ֱ��д�����ۣ�
�Բ���BD��AC��������ϵ����ֱ��д�����ۣ�
![]() �������BD��AC�ļнǶ���������ܣ���ֱ��д���нǶ�����������ܣ���˵�����ɣ�
�������BD��AC�ļнǶ���������ܣ���ֱ��д���нǶ�����������ܣ���˵�����ɣ�
���𰸡�(1)������;(2)������;(3) ��BD=AC���ɼ�����;![]() ��������
��������
��������
��1������֤����BDE�ա�ACE�Ƴ�BD=AC��BD��AC��
��2����ͼ2�У��������仯��ֻҪ֤����BED�ա�AEC���Ƴ�BD=AC����BDE=��ACE���ɡ�DEC=90�㣬�Ƴ���ACE+��EOC=90�㣬��Ϊ��EOC=��DOF�����ԡ�BDE+��DOF=90�㣬�ɵá�DFO=180�㣭90��=90�㣬����֤����
��3������ͼ3�У����ۣ�BD=AC��ֻҪ֤����BED�ա�AEC���ɣ�
���ܣ��ɡ�BED�ա�AEC��֪����BDE=��ACE���Ƴ���DFC=180�㣭����BDE+��EDC+��DCF��=180�㣭����ACE+��EDC+��DCF��=180�㣭��60��+60�㣩=60�㼴�ɽ�����⣮
�⣺![]() ��
��![]() ��
��
�����ǣ��ӳ�BD��AC��F��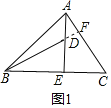
![]() ��
�� ![]() ��
��
��![]() ��
��![]() ��
��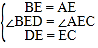
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �������仯��
�������仯��
��ͼ2����AC��DE����ΪO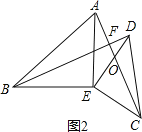
���ɣ�![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��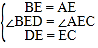
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
(3)![]() ��
��
֤����![]() ��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��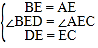
![]() ��
��![]() ��
��![]() ��
��
�ڼн�Ϊ![]() ��
��
�⣺��ͼ3����AC��BD����ΪF��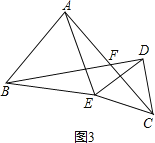
�ɢ�֪![]() ��
��![]() ��
��![]() ��
��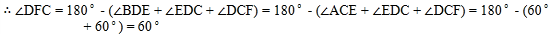 ����BD��AC���ɵĽǵĶ���Ϊ
����BD��AC���ɵĽǵĶ���Ϊ![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
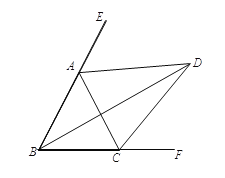
����Ŀ����ͼ����ABC=��ACB��AD��BD��CD�ֱ�ƽ�֡�ABC����ǡ�EAC���ڽǡ�ABC����ǡ�AFC�����½��ۣ���AD��BC���ڡ�ACB=2��ADB���ۡ�ADC=90�㡪��ABD���ܡ�BDC=![]() ��BAC��������ȷ�Ľ�����_____________��
��BAC��������ȷ�Ľ�����_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�����P��A���������ÿ��1����λ���ȵ��ٶ���AB��B���˶���ͬʱ����Q��B���������ÿ��2����λ���ȵ��ٶ���BC��CD�����˶�����P�˶���B��ʱ��P��Q����ͬʱֹͣ�˶�����P���˶���ʱ��Ϊt����APQ�����ΪS����S��t�ĺ�����ϵ��ͼ���ǡ� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С��7������ͼ��һ�κ���![]() ��ͼ����x�ύ�ڵ�B���뷴��������
��ͼ����x�ύ�ڵ�B���뷴��������![]() ��ͼ���һ������ΪA��2��m����
��ͼ���һ������ΪA��2��m����

��1�����������ı���ʽ��
��2������x����ʲô��Χʱ��![]() ��
��![]() ��
��
��3������A��AC��x��������Ϊ��C���������P�ڷ���������ͼ����������PBC���������6����ֱ��д����P��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() Ϊ����
����![]()
![]() ��
��![]() ����֤�ú���ͼ����x����н���
����֤�ú���ͼ����x����н���
![]() ��֤������mΪ��ֵ���ú���ͼ��Ķ��㶼�ں���
��֤������mΪ��ֵ���ú���ͼ��Ķ��㶼�ں���![]() ��ͼ����
��ͼ����
![]() ��
��![]() ʱ��y����СֵΪ
ʱ��y����СֵΪ![]() ����m��ֵ
����m��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
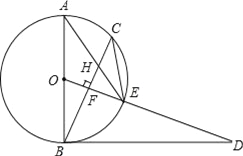
����Ŀ����֪����ͼ��AB�ǡ�O��ֱ������CΪ��O��һ�㣬OF��BC�ڵ�F������O�ڵ�E��AE��BC���ڵ�H����DΪOE���ӳ�����һ�㣬�ҡ�ODB=��AEC��
��1����֤��BD�ǡ�O�����ߣ�
��2����֤��CE2=EHEA��
��3������O�İ뾶Ϊ5��sinA=![]() ����BH�ij���
����BH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��AB�ϣ���E��AC�ϣ�BE��CD�ཻ�ڵ�O.
��1������A=50������BOD=70������C=30�������B�Ķ�����
��2���Բ����BOC���A+��B+��C֮��Ĺ�ϵ����֤����������ȷ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڳ�����ABCD�У�AB=4��AD=6���ӳ�BC����E��ʹCE=2������DE������P�ӵ�B��������ÿ��2����λ���ٶ���BC��CD��DA���յ�A�˶������P���˶�ʱ��Ϊt�룬��t��ֵΪ_____��ʱ����ABP����DCEȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ĵ���ͼ����Ӧ�ĵ�ʽ��̽�����еĹ��ɣ�
![]() ����۲죬����
����۲죬����![]() ����ĺ�����д����Ӧ�ĵ�ʽ��
����ĺ�����д����Ӧ�ĵ�ʽ��

![]() ��
��![]() ��
��![]() ��
��![]() ______
______![]()
![]() ���
���![]() �۲����е���ͼ������
�۲����е���ͼ������![]() ����ĺ�����д����Ӧ�ĵ�ʽ��
����ĺ�����д����Ӧ�ĵ�ʽ��

![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ______
______![]()
![]() ����
����![]() �еĵ�n������ͼб�ߵ����Ϸ�����36���㣬�����n������ͼ���ܹ��ж��ٸ��㣮
�еĵ�n������ͼб�ߵ����Ϸ�����36���㣬�����n������ͼ���ܹ��ж��ٸ��㣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com