
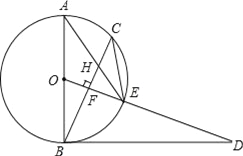
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA=![]() ,求BH的长.
,求BH的长.
【答案】(1)证明见解析;(2)证明见解析;(3)BH=![]() .
.
【解析】试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出![]() ,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论;
,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图1所示:
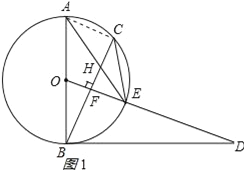
∵OF⊥BC,
∴![]() ,
,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴![]() ,
,
∴CE2=EHEA;
(3)解:连接BE,如图2所示:
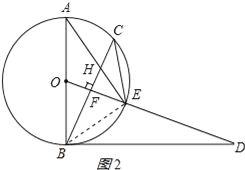
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE=![]() ,
,
∴AB=10,BE=ABsin∠BAE=10×![]() =6,
=6,
∴EA=![]() =
=![]() =8,
=8,
∵![]() ,
,
∴BE=CE=6,
∵CE2=EHEA,
∴EH=![]() =
=![]() ,
,
在Rt△BEH中,BH=![]() =
=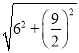 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文1张、数学2张、英语1张
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年全国两会于3月5日至20日在北京召开,为了了解市民“获取两会新闻的最主要途径”,记者小李开展了一次抽样调查,根据调查结果绘制了如图所示尚不完整的统计图.根据图中信息解答下列问题:

(1)这次接受调查的市民总人数是 ;
(2)扇形统计图中,“电视”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有700万人,请你估计其中将“电脑上网和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC>BA,AD=DC,

(1)若BD⊥CD,∠C=60°,BC=10,求AD的长;
(2)若BD平分∠ABC,求证:∠A+∠C=180°。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:一个点将一条直线分为两段,如果其中较长的一段与整个线段的比等于较短一段与较长一段的比,我们就说这个点是这条线段的黄金分割点,较长的一段与整个线段的比值![]() 或较短一段与较长一段的比值
或较短一段与较长一段的比值![]() 叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是
叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是![]() 我国国旗上的正五角星中就存在黄金分割点
我国国旗上的正五角星中就存在黄金分割点![]() 解决问题:
解决问题:
![]() 如图,已知A、B、C、D、E是
如图,已知A、B、C、D、E是![]() 的五等分点,求
的五等分点,求![]() 的度数;
的度数;
![]() 若AC、AD分别与BE交于点M、
若AC、AD分别与BE交于点M、![]() 求证:点M是线段BN的一个黄金分割点.
求证:点M是线段BN的一个黄金分割点.
![]() 若
若![]() ,则
,则![]() ______
______![]() 若有根号保留根号
若有根号保留根号![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com