【题目】等腰三角形的一条高与一腰的夹角为40°，则等腰三角形的一个底角为_____．
【答案】50°或65°或25°
【解析】
分高为底边上的高和腰上的高两种情况，腰上的高再分是锐角三角形和钝角三角形两种情况讨论求解．
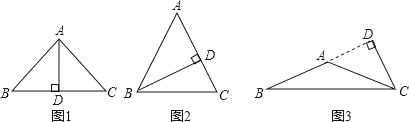
解：如图1，高为底边上的高时，∵∠BAD＝40°，
∴顶角∠BAC＝2∠BAD＝2×40°＝80°，
底角为（180°﹣80°）÷2＝50°；
高为腰上的高时，如图2，若三角形是锐角三角形，
∵∠ABD＝40°，
∴顶角∠A＝90°﹣40°＝50°，
底角为（180°﹣50°）÷2＝65°；
如图3，若三角形是钝角三角形，
∵∠ACD＝40°，
∴顶角∠BAC＝∠ACD+∠D＝40°+90°＝130°，
底角为（180°﹣130°）÷2＝25°．
综上所述，等腰三角形的一个底角为50°或65°或25°．
故答案为：50°或65°或25°．
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案科目：初中数学 来源： 题型：
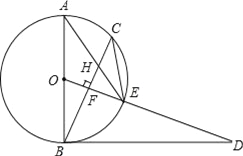
【题目】已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．
（1）求证：BD是⊙O的切线；
（2）求证：CE2=EHEA；
（3）若⊙O的半径为5，sinA=
，求BH的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，半径为1个单位长度的半圆O1，O2，O3，…组成一条平滑曲线，点P从点O出发，沿这条曲线向右运动，速度为每秒 
个单位长度，则第2016秒时，点P的坐标是（ ）
A.（2015,0）B.（2015，-1）C.（2016,0）D.（2016，-1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为_____秒时，△ABP和△DCE全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】仔细阅读下面例题，解答问题：例题: 已知二次三项式x2 4x m 有一个因式是 ( x 3) ，求另一个因式以及 m 的值.
解：设另一个因式为 ( x n) ，得x2 4x m ( x 3) ( x n)
则x2 4 x m x2 (n 3) x 3n
∴
解得： n 7, m 21
∴ 另一个因式为 ( x 7) ， m 的值为－21 .
问题：仿照以上方法解答下面问题：
（1）已知二次三项式2x2+3x-k有一个因式是（2x-5），求另一个因式以及k的值．
（2）已知二次三项式6x2+4ax+2有一个因式是（2x+a），a是正整数，求另一个因式以及a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
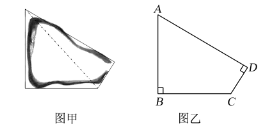
【题目】如图是我国某海域内的一个小岛，其平面图如图甲所示，小明据此构造出该岛的一个数学模型如图乙所示，其中∠B＝∠D＝90°，AB＝BC＝15千米，CD＝3
千米，请据此解答如下问题：
(1)求该岛的周长和面积；(结果保留整数，参考数据：≈1.414，
≈1.732，
≈2.449)
(2)求∠ACD的余弦值．
查看答案和解析>>
科目：初中数学 来源： 题型：
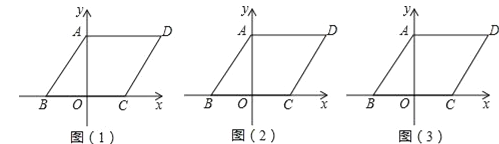
【题目】如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根，且OA＞OB．
（1）求A、B的坐标．
（2）求证：射线AO是∠BAC的平分线．
（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，直接写出F点的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销 x 件，已知产销两种产品的有关信息 如下：
产品 | 每件售价/万元 | 每件成本/万元 | 年最大产销量/件 |
甲 | 6 | 3 | 200 |
乙 | 20 | 10 | 80 |
甲、乙两产品每年的其他费用与产销量的关系分别是： y1 kx b 和 y2 ax2 m ，它们的函数图象分别如图（1）和图（2）所示.
（1）求： y1 、 y2 的函数解析式；
（2）分别求出产销两种产品的最大利润；（利润=销售额-成本-其它费用）
（3）若通过技术改进，甲产品的每件成本降到 a 万元，乙产品的年最大产销量可以达到 110 件，其它都不变，为获得最大利润，该公式应该选择产销哪种产品？请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
