
【题目】如图是我国某海域内的一个小岛,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠B=∠D=90°,AB=BC=15千米,CD=3![]() 千米,请据此解答如下问题:
千米,请据此解答如下问题:
(1)求该岛的周长和面积;(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
(2)求∠ACD的余弦值.
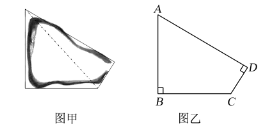
【答案】(1) 周长:55千米,面积:157平方千米;(2)![]() .
.
【解析】
(1)连接AC,根据AB=BC=15千米,∠B=90°得到∠BAC=∠ACB=45° ,AC=15![]() 千米,再根据∠D=90°利用勾股定理求得AD的长后即可求周长和面积;
千米,再根据∠D=90°利用勾股定理求得AD的长后即可求周长和面积;
(2)直接利用余弦的定义求解即可
(1)连接AC
∵AB=BC=15千米,∠B=90°
∴∠BAC=∠ACB=45° AC=15![]() 千米
千米
又∵∠D=90°
∴AD=![]() (千米)
(千米)
∴周长=AB+BC+CD+DA=30+3![]() +12
+12![]() =30+4.242+20.784≈55(千米)
=30+4.242+20.784≈55(千米)
面积=S△ABC+S△ADC=112.5+18![]() ≈157(平方千米)
≈157(平方千米)
(2)cos∠ACD=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC>BA,AD=DC,

(1)若BD⊥CD,∠C=60°,BC=10,求AD的长;
(2)若BD平分∠ABC,求证:∠A+∠C=180°。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,∠BAC=30°,AB=AC,∠PAB=α,点B关于直线AP的对称点为点D,连接AD,连接BD交AP于点G,连接CD交AP于点E,交AB于点F.
(1)如图当α=15°时,①按要求画出图形,②求出∠ACD的度数,③探究DE与BF的倍数关系并加以证明;
(2)在直线AP绕点A顺时针旋转的过程中(0°<α<75°),当△AEF为等腰三角形时,画出相应图形直接求出α的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
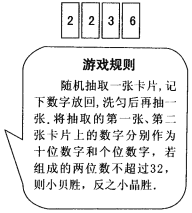
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:一个点将一条直线分为两段,如果其中较长的一段与整个线段的比等于较短一段与较长一段的比,我们就说这个点是这条线段的黄金分割点,较长的一段与整个线段的比值![]() 或较短一段与较长一段的比值
或较短一段与较长一段的比值![]() 叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是
叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是![]() 我国国旗上的正五角星中就存在黄金分割点
我国国旗上的正五角星中就存在黄金分割点![]() 解决问题:
解决问题:
![]() 如图,已知A、B、C、D、E是
如图,已知A、B、C、D、E是![]() 的五等分点,求
的五等分点,求![]() 的度数;
的度数;
![]() 若AC、AD分别与BE交于点M、
若AC、AD分别与BE交于点M、![]() 求证:点M是线段BN的一个黄金分割点.
求证:点M是线段BN的一个黄金分割点.
![]() 若
若![]() ,则
,则![]() ______
______![]() 若有根号保留根号
若有根号保留根号![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com