
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
(1)求A、B的坐标.
(2)求证:射线AO是∠BAC的平分线.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
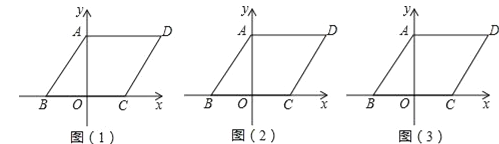
【答案】(1)A(0,4),B(﹣3,0)(2)射线AO是∠BAC的平分线(3)满足条件的点有四个:F1(3,8);F2(﹣3,0);F3(﹣![]() ,﹣
,﹣![]() );F4(﹣
);F4(﹣![]() ,
, ![]() ).
).
【解析】试题分析:(1)先解出一元二次方程,即得出OA,OB,即可得出点A,B坐标;
(2)先得出BC=AD=6,求出OC,再判断出△AOB≌△AOC即可;
(3)根据菱形的性质,分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况,以及AC与AF分别是对角线的情况分别进行求解计算.
试题解析:解:(1)∵关于x的一元二次方程x2﹣7x+12=0的两个根,∴x=3或x=4,∵OA>OB,∴OA=4,OB=3,∴A(0,4),B(﹣3,0);
(2)∵四边形ABCD是平行四边形,∴BC=AD=6,∵B(﹣3,0),∴C(3,0),∴OC=OB,在△AOB和△AOC中,∵OB=OC,∠AOB=∠AOC,AO=AO,∴△AOB≌△AOC,∴∠BAO=∠CAO,∴射线AO是∠BAC的平分线
(3)∵OB=OC=3,∴AO平分∠BAC.
①AC、AF是邻边,点F在射线AB上时,AF=AC=5,所以点F与B重合,即F(﹣3,0);
②AC、AF是邻边,点F在射线BA上时,M应在直线AD上,且FC垂直平分AM,点F(3,8).
③AC是对角线时,做AC垂直平分线L,AC解析式为y=﹣![]() x+4,直线L过(
x+4,直线L过(![]() ,2),且k值
,2),且k值![]() (平面内互相垂直的两条直线k值乘积为﹣1),L解析式为
(平面内互相垂直的两条直线k值乘积为﹣1),L解析式为![]() ,联立直线L与直线AB求交点,∴F(﹣
,联立直线L与直线AB求交点,∴F(﹣![]() ,﹣
,﹣![]() );
);
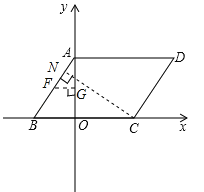
④AF是对角线时,过C做AB垂线,垂足为N,
根据等积法求出CN=![]() ,勾股定理得出,AN=
,勾股定理得出,AN=![]() ,作A关于N的对称点即为F,AF=
,作A关于N的对称点即为F,AF=![]() ,过F做y轴垂线,垂足为G,FG=
,过F做y轴垂线,垂足为G,FG=![]() ,∴F(﹣
,∴F(﹣![]() ,
, ![]() ).
).
综上所述,满足条件的点有四个:F1(3,8);F2(﹣3,0);F3(﹣![]() ,﹣
,﹣![]() );F4(﹣
);F4(﹣![]() ,
, ![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文1张、数学2张、英语1张
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
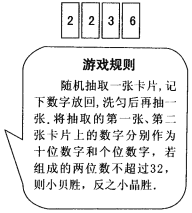
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于点E,

(1)求证:DE=AE+BC .
(2)若![]() ,求线段AE的长.
,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:一个点将一条直线分为两段,如果其中较长的一段与整个线段的比等于较短一段与较长一段的比,我们就说这个点是这条线段的黄金分割点,较长的一段与整个线段的比值![]() 或较短一段与较长一段的比值
或较短一段与较长一段的比值![]() 叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是
叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是![]() 我国国旗上的正五角星中就存在黄金分割点
我国国旗上的正五角星中就存在黄金分割点![]() 解决问题:
解决问题:
![]() 如图,已知A、B、C、D、E是
如图,已知A、B、C、D、E是![]() 的五等分点,求
的五等分点,求![]() 的度数;
的度数;
![]() 若AC、AD分别与BE交于点M、
若AC、AD分别与BE交于点M、![]() 求证:点M是线段BN的一个黄金分割点.
求证:点M是线段BN的一个黄金分割点.
![]() 若
若![]() ,则
,则![]() ______
______![]() 若有根号保留根号
若有根号保留根号![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示为一个无盖的正方体纸盒,现将其展开成平面图,如图(2)所示.已知展开图中每个正方形的边长为1:

(1)在展开图(2)中可画出最长线段的长度为 ,在平面展开图(2)中这样的最长线段一共能画出 条。
(2)试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com