练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，∠ACB=90°，AC=BC，D为△ABC外一点，且AD=BD，DE⊥AC交CA的延长线于点E，

    （1）求证：DE=AE+BC .

    （2）若，求线段AE的长.

    【答案】（1）见详解；（2）1

    【解析】

    （1）连接CD，利用垂直平分线的判定即可得CD垂直平分AB，再利用三线合一得到∠ACD=∠ACB，然后证出△ECD为等腰直角三角形得到DE=EC即可.

    （2）先证△CAD≌△CBD，可得S △CAD= S△CBD=，再利用三角形的面积和高求出底AC，再利用（1）的结论就可求出AE.

    （1）连接CD

    ∵AC=BC，AD=BD

    ∴点C和点D都在AB垂直平分线上

    ∴CD垂直平分AB

    ∴CD平分∠ACB

    ∵∠ACB=90°

    ∴∠ACD=∠ACB=45°

    ∵DE⊥AC

    ∴△ECD为等腰直角三角形，DE=EC

    ∵EC=AE＋AC= AE＋BC

    ∴DE=AE+BC.

    （2）在△CAD和△CBD中

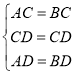
    ∴△CAD≌△CBD（SSS）

    ∴S△CAD= S△CBD=

    ∵DE=3

    ∴AC=2 S△CAD÷DE=2

    ∵DE= EC=AE+AC

    ∴AE= DE－AC=1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形ABC中，AB=AC=BC=10cm，DC=4cm。如果点M、N都以3cm/s的速度运动，点M在线段CB上由点C向点B运动，点N在线段BA上由点B向点A运动。它们同时出发，当两点运动时间为t秒时，△BMN是一个直角三角形，则t的值为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】仔细阅读下面例题，解答问题：例题: 已知二次三项式x2 4x m 有一个因式是 ( x 3) ，求另一个因式以及 m 的值.

    解：设另一个因式为 ( x n) ，得x2 4x m ( x 3) ( x n)

    则x2 4 x m x2 (n 3) x 3n

    ∴

    解得： n 7, m 21

    ∴ 另一个因式为 ( x 7) ， m 的值为－21 .

    问题：仿照以上方法解答下面问题：

    （1）已知二次三项式2x2+3x-k有一个因式是（2x-5），求另一个因式以及k的值．
    （2）已知二次三项式6x2+4ax+2有一个因式是（2x+a），a是正整数，求另一个因式以及a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在中，，，是过点的一条直线，且点在线段上时，于点，于点.易证：.

    （1）如图②，点在线段的延长线时，其余条件不变，问与，的关系如何？请证明；

    （2）如图③，点在线段的延长线时，其余条件不变，问与的关系如何？请直接写出结果，不需证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根，且OA＞OB．

    （1）求A、B的坐标．

    （2）求证：射线AO是∠BAC的平分线．

    （3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，直接写出F点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知:如图， △ABC中，AB=AC,D在AC上,E在BC上，A E,B D交于F,∠AFD=60°，∠FDC+∠FEC=180°.

    (1)求证：BE=CD.

    (2)如图2，过点D作DG⊥AF于G，直接写出AE ，FG, BF的关系.

    (3)如图3，在(2)的条件下,连接CG,若FG=BF，△AGD的面积等于5，求GC的长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，方格纸中每个小方格都是边长为1个单位的正方形，若学校位置坐标为A（2，1），图书馆位置坐标为B（﹣1，﹣2），解答以下问题：

    （1）在图中标出平面直角坐标系的原点，并建立直角坐标系；

    （2）若体育馆位置坐标为C（1，﹣3），请在坐标系中标出体育馆的位置；

    （3）顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,则AE的长为( )

    A. 2或3 B. 或 C. 或 D. 3或4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a、b、c为ABC的内角A、B、C所对应的边，满足下列条件的三角形不是直角三角形的是

    A. ∠C=∠A∠BB. a:b:c = 1 : :

    C. ∠A∶∠B∶∠C＝5∶4∶3D. ，

    查看答案和解析>>

    同步练习册答案