
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
【答案】(1) 甲商品每件进价为30元,乙商品每件进价为70元;(2) 最大的进货方程是购买甲种商品80件,乙种商品20件,最大利润为1200元.
【解析】
(1)设甲商品每件进价为x元,乙商品每件进价为y元,根据甲商品2件和乙商品3件共需270元,甲商品3件和乙商品2件共需230元,列出方程求解即可;
(2)根据题意可以得到利润与甲种商品的关系,由甲种商品的数量不少于乙种商品数量的4倍,可以得到甲种商品的取值范围,从而可以求得获利最大的进货方案,以及最大利润.
解:(1)设甲商品每件进价为x元,乙商品每件进价为y元,
![]()
解得:![]()
∴甲商品每件进价为30元,乙商品每件进价为70元.
(2)设购买甲种商品a件,获利为w元,
![]()
∵![]() ,
,
解得:![]() ,
,
当a=80时,w取得最大值,所以w=1200,
∴最大的进货方程是购买甲种商品80件,乙种商品20件,最大利润为1200元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点D、E分别是△ABC两边AB、BC所在直线上的点,∠BDE+∠ACB=180°,DE=AC,AD=2BD.


(1) 如图1,当点D、E分别在AB、CB的延长线上时,求证:BE=BD
(2) 如图2,当点D、E分别在AB、BC边上时,BE与BD存在怎样的数量关系?请写出你的结论,并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
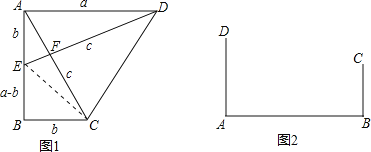
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的电脑,已知购买一台A型电脑需0.6万元,购买一台B型电脑需0.4万元,该公司准备投入资金y万元,全部用于购进35台这两种型号的电脑,设购进A型电脑x台.
(1)求y关于x的函数解析式;
(2)若购进B型电脑的数量不超过A型电脑数量的2倍,则该公司至少需要投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 延长线上的一点,点
延长线上的一点,点![]() 是
是![]() 的中点。
的中点。

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作![]() 的平分线
的平分线![]() . ②连接
. ②连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(2)猜想与证明:试猜想![]() 与
与![]() 有怎样的关系,并说明理由。
有怎样的关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)求证:BC平分∠DBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
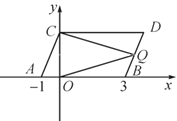
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为【 】

A.1 B.![]() C. 2 D.
C. 2 D.![]() +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com