
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为【 】

A.1 B.![]() C. 2 D.
C. 2 D.![]() +1
+1
【答案】B。
【解析】分两步
(1)若点P,Q固定,此时点K的位置:如图,作点P关于BD的对称点P1,连接P1Q,交BD于点K1。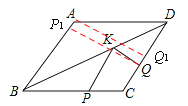
由线段中垂线上的点到线段两端距离相等的性质,得
P1K1 = P K1,P1K=PK。
由三角形两边之和大于第三边的性质,得P1K+QK>P1Q= P1K1+Q K1= P K1+Q K1。
∴此时的K1就是使PK+QK最小的位置。
(2)点P,Q变动,根据菱形的性质,点P关于BD的对称点P1在AB上,即不论点P在BC上任一点,点P1总在AB上。
因此,根据直线外一点到直线的所有连线中垂直线段最短的性质,得,当P1Q⊥AB时P1Q最短。
过点A作AQ1⊥DC于点Q1。 ∵∠A=120°,∴∠DA Q1=30°。
又∵AD=AB=2,∴P1Q=AQ1=AD·cos300=![]() 。
。
综上所述,PK+QK的最小值为![]() 。故选B。
。故选B。


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有( )
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;③∠BIC=90°+![]() ∠BAC;
∠BAC;
④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.
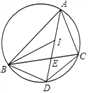
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是对角线AC上一点(不与点A、C重合),连接PD,过点P作PE⊥PD交射线BC于点E.
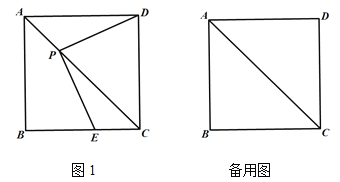
(1)如图1,求证:PD=PE;
(2)若正方形ABCD的边长为4,![]() ,求CE长.
,求CE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
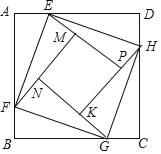
A. 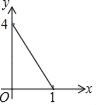 B.
B. 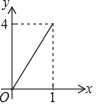 C.
C. 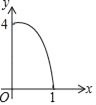 D.
D. 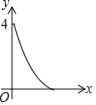
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
1 | ° | x | 7 | ﹣3 | … |
(1)可知x= ,= ,°= ;
(2)试判断第2016个格子中的数是多少?并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2016?若能,求出n的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为筹备校庆活动,准备印刷一批校庆纪念册,该纪念册每册需要10张同样大小的纸,其中4张为彩页,6张为黑白页,印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为彩页300元/张,黑白页50元/张,印刷费与印数的关系见下表:
印数 |
|
|
彩色(单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
求:(1)印刷这批纪念册的制版费为多少元?
(2)若印刷2千册,则共需多少费用?
(3)如果该校希望印数![]() 至少为4千册,总费用为
至少为4千册,总费用为![]() 元,请用含有
元,请用含有![]() 的式子表示总费用?
的式子表示总费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
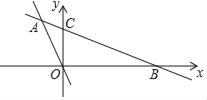
【题目】如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于点B、C,与直线OA交于点A.已知点A的坐标为(﹣3,5),OC=4.
(1)分别求出直线AB、AO的解析式;
(2)求△ABO的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com