
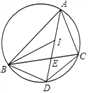
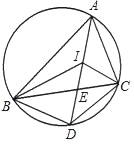
【题目】如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有( )
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;③∠BIC=90°+![]() ∠BAC;
∠BAC;
④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题解析:①∵I是△ABC的内心,
∴AI平分∠BAC,
∴∠CAD=∠DAB,
∴∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
所以此选项说法正确;
②∵I是△ABC的内心,
∴I是△ABC三个角平分线的交点,
∴I到△ABC三边的距离相等,
所以此选项说法不正确;
③∵I是内心,
∴BI、CI分别平分∠ABC、∠ACB,
∴∠ABI=![]() ∠ABC,∠ACI=
∠ABC,∠ACI=![]() ∠ACB,
∠ACB,
∵∠BIE=∠ABI+∠BAI,∠EIC=∠DAC+∠ACI,
∴∠BIC=∠BIE+∠EIC=∠ABI+∠BAI+∠DAC+∠ACI,
∵∠ABC+∠ACB=180°﹣∠BAC,
∴![]() ∠ABC+
∠ABC+![]() ∠ACB=90°﹣
∠ACB=90°﹣![]() ∠BAC,
∠BAC,
∴∠ABI+∠ACI=90°﹣![]() ∠BAC,
∠BAC,
∴∠BIC=90°﹣![]() ∠BAC+∠BAC=90°+
∠BAC+∠BAC=90°+![]() ∠BAC,
∠BAC,
所以此选项说法正确;
④∵∠DCB=∠BAD,∠BAD=∠DAC,
∴∠DCB=∠DAC,
∵∠ADC=∠ADC,
∴△ADC∽△CDE,
∴![]() ,
,
∴DC2=DEAD,
∵∠DIC=∠DAC+∠ACI,∠DCI=∠ICB+∠DCB,
∵IC平分∠ACB,
∴∠ACI=∠ICB,
∴∠DIC=∠DCI,
∴DC=DI,
∴DI2=DEAD,
∴线段DI是线段DE与DA的比例中项;
所以此选项说法正确;
⑤∵∠BAD=∠DAC,∠BAD=∠DCB,∠DAC=∠DBC,
∴∠DCB=∠DBC,
∴DB=DC,
由④得:DC=DI,
∴DB=DC=DI,
∴点D是△BIC的外心;
所以此选项说法正确;
所以说法正确的有:①③④⑤;
故选D.


科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
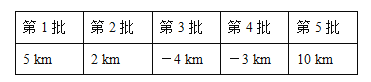
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人和人之间讲友情,有趣的是,数与数之间也有相类似的关系. 若两个不同的自然数的所有真因数(即除了自身以外的正约数)之和相等,我们称这两个数为“亲和数”. 例如:18的约数有1、2、3、6、9、18,它的真因数之和1+2+3+6+9=21;51的约数有1、3、17、51,它的真因数之和1+3+17=21,所以18和51为“亲和数”. 数还可以与动物形象地联系起来,我们称一个两头(首位与末位)都是![]() 的数为“两头蛇数”.
的数为“两头蛇数”.
(1)6的“亲和数”为 ;将一个四位的“两头蛇数”去掉两头,得到一个两位数,它恰好是这个“两头蛇数”的约数,求满足条件的“两头蛇数”.
(2)已知两个“亲和数”的真因数之和都等于15,且这两个“亲和数”中较大的数能将一个正中间数位(百位)上的数为4的五位“两头蛇数”整除,若这个五位“两头蛇数”的千位上的数字小于十位上的数字,求满足条件的“两头蛇数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2![]() =2×
=2×![]() +1,5
+1,5![]() =5×
=5×![]() +1,给出定义如下:我们称使等式ab=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式ab=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)判断数对(2,1),(3,![]() )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;
(2)若(a,3)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则(n,m)“共生有理数对”(填“是”或“不是”);说明理由;
(4)请再写出一对符合条件的“共生有理数对”为(注意:不能与题目中已有的“共生有理数对”重复).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算.比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求3⊕(﹣2)的值;
(2)若3⊕x的值小于16,求x的取值范围,并在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答会告诉你方法.
(1)阅读下列材料:
问题:利用一元一次方程将![]() 化成分数.
化成分数.
解:设![]() .
.
方程两边都乘以10,可得![]() .
.
由![]() 和
和![]() ,可得
,可得
![]() 即
即![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
解得![]() ,即
,即![]() .
.
填空:将![]() 写成分数形式为 .
写成分数形式为 .
(2)请你仿照上述方法把小数![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC,AC=BC=13,把△ABC放在平面直角坐标系中,且点A、B的坐标分别为(2,0)、(12,0),将△ABC沿x轴向左平移,当点C落在直线y=-x+8上时,线段AC扫过的面积为_____;
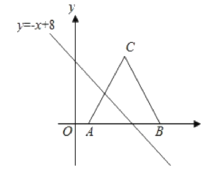
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为【 】

A.1 B.![]() C. 2 D.
C. 2 D.![]() +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com