练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某出租车司机从公司出发，在东西方向的人民路上连续接送5批客人，行驶路程记录如下(规定向东为正，向西为负，单位：km)：

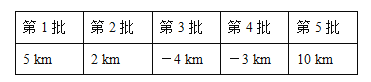
    （1）接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？

    （2）若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

    （3）若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

    【答案】（1）10千米；在出发点东侧;（2）4.8L;（3）车费68元

    【解析】

    （1）根据有理数加法即可求出答案.

    （2）根据题意列出算式即可求出答案.

    （3）根据题意列出算式即可求出答案.

    （1）5+2+（-4）+（-3）+10=10（km）

    答：接送完第五批客人后，该驾驶员在公司的东边10千米处.

    （2）（5+2+｜-4｜+｜-3｜+10）×0.2=24×0.2=4.8（升）

    答：在这个过程中共耗油4.8升.

    （3）[10+(5-3) ×1.8]+10+[10+(4-3) ×1.8]+10+[10+(10-3) ×1.8]=68（元）

    答：在这个过程中该驾驶员共收到车费68元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知长方形纸片，点在边上，点在边上，将沿翻折到，射线与交于点.点在边上，将沿翻折到，射线与交于点.

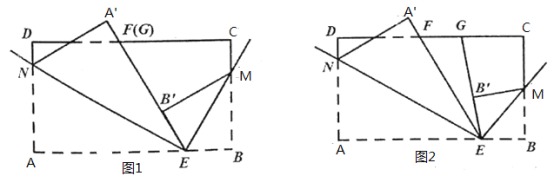
    （1）如图1，若点与点重合，直接写出以为顶点的两对相等的角，并求的度数；

    （2）如图2，若点在点的右侧，且，，求与的度数；

    （3）若点在点的左侧，且，求的度数（用含的代数式表示）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在解决问题：已知a=，求2a2﹣8a+1的值，他是这样分析与解的：

    ∵a===2﹣

    ∴a﹣2=﹣

    ∴（a﹣2）2=3，a2﹣4a+4=3

    ∴a2﹣4a=﹣1

    ∴2a2﹣8a+1=2（a2﹣4a）+1=2×（﹣1）+1=﹣1

    请你根据小明的分析过程，解决如下问题：

    （1）化简+++…+

    （2）若a=，求4a2﹣8a+1的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．试探索BF与CF的数量关系，写出你的结论并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线与直线垂直相交于点，点在射线上运动（点不与点重合），点在射线上运动（点不与点重合）.

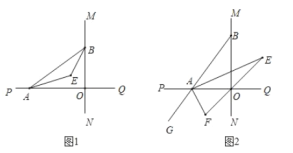
    (1)如图1，已知、分别是和的角平分线，

    ①当时，求的度数；

    ②点在运动的过程中，的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出的大小；

    (2)如图2，延长至，已知、的角平分线与的角平分线所在的直线分别相交于、，在中，如果有一个角是另一个角的3倍，请直接写出的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B、C三瓶不同浓度的酒精，A瓶内有酒精2kg，浓度x%，B瓶有酒精3kg，浓度y%，C瓶有酒精5kg，浓度z%，从A瓶中倒出10%，B瓶中倒出20%，C瓶中倒出24%，混合后测得浓度33.5%，将混合后的溶液倒回瓶中，使它们恢复原来的质量，再从A瓶倒出30%，B瓶倒出30%，C瓶倒出30%，混合后测得浓度为31.5%，测量发现，，，且x、y、z均为整数，则把起初A、B两瓶酒精全部混合后的浓度为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：若a，b都是非负实数，则a+b≥2．当且仅当a=b时，“=”成立．

    证明：∵（）2≥0，∴a-2+b≥0．

    ∴a+b≥2．当且仅当a=b时，“=”成立．

    举例应用：已知x＞0，求函数y=x的最小值．

    解：y=x=2．当且仅当x=，即x=时，“=”成立．

    ∴当x=时，函数取得最小值，y最小=2．

    问题解决：

    （1）已知x＞0，求函数y=的最小值；

    （2）求代数式（m＞-1）的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

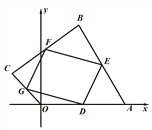
    【题目】如图，在平面直角坐标系xOy中，四边形OABC的顶点A在x轴的正半轴上，OA=4，OC=2，点D、E、F、G分别为边OA、AB、BC、CO的中点，连结DE、EF、FG、GD.

    （1）若点C在y轴的正半轴上，当点B的坐标为（2，4）时，判断四边形DEFG的形状，并说明理由.

    （2）若点C在第二象限运动，且四边形DEFG为菱形时，求点四边形OABC对角线OB长度的取值范围.

    （3）若在点C的运动过程中，四边形DEFG始终为正方形，当点C从X轴负半轴经过Y轴正半轴，运动至X轴正半轴时，直接写出点B的运动路径长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】鸡兔同笼问题是我国古代著名趣题之一，大约在 1500 年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡、兔同在一个笼子里，从上上面数，有 35 个头；从下面数，有 94 只脚 ．求笼中各有几只鸡和兔？经计算可得（ ）

    A. 鸡 20 只，兔 15 只 B. 鸡 12 只，兔 23 只

    C. 鸡 15 只，兔 20 只 D. 鸡 23 只，兔 12 只

    查看答案和解析>>

    同步练习册答案