
【题目】已知长方形纸片![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折到
翻折到![]() ,射线
,射线![]() 与
与![]() 交于点
交于点![]() .点
.点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折到
翻折到![]() ,射线
,射线![]() 与
与![]() 交于点
交于点![]() .
.
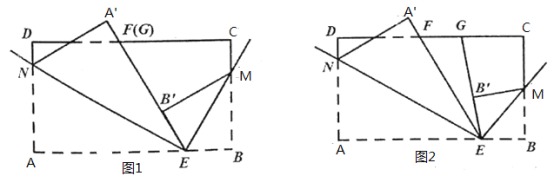
(1)如图1,若点![]() 与点
与点![]() 重合,直接写出以
重合,直接写出以![]() 为顶点的两对相等的角,并求
为顶点的两对相等的角,并求![]() 的度数;
的度数;
(2)如图2,若点![]() 在点
在点![]() 的右侧,且
的右侧,且![]() ,
,![]() ,求
,求![]() 与
与![]() 的度数;
的度数;
(3)若点![]() 在点
在点![]() 的左侧,且
的左侧,且![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)∠AEN=∠NEF,∠BEM=∠FEM;∠MEN=90°;(2)∠FEG=24°,∠MEN=102°;(3)∠MEN=90°-![]() α.
α.
【解析】
(1)根据折叠的性质,平角的定义,角的和差定义计算即可;
(2)根据折叠的性质以及平角的定义,可得出∠AEN +∠BEM=![]() (180°-∠FEG),再结合所给的两个等式可得出∠FEG的度数;根据∠MEN=180°-(∠AEN+∠BEM),求出∠AEN+∠BEM即可解决问题;
(180°-∠FEG),再结合所给的两个等式可得出∠FEG的度数;根据∠MEN=180°-(∠AEN+∠BEM),求出∠AEN+∠BEM即可解决问题;
(3)先画出图形,根据(2)中的思路即可分析出∠MEN与∠FEG之间的等量关系,即可得出结果.
解:(1)根据折叠的性质可得,
以E为顶点的两对相等的角分别为: ∠AEN=∠NEF,∠BEM=∠FEM.
∴∠NEF=![]() ∠AEF,∠MEF=
∠AEF,∠MEF=![]() ∠BEF,
∠BEF,
∴∠MEN=∠NEF+∠MEF=![]() ∠AEF+
∠AEF+![]() ∠BEF=
∠BEF=![]() (∠AEF+∠BEF)=
(∠AEF+∠BEF)=![]() ∠AEB,
∠AEB,
∵∠AEB=180°,
∴∠MEN=![]() ×180°=90°;
×180°=90°;
(2)由(1)可得∠AEN=![]() ∠AEF,∠BEM=
∠AEF,∠BEM=![]() ∠BEG,
∠BEG,
∴∠AEN +∠BEM =![]() ∠AEF+
∠AEF+![]() ∠BEG=
∠BEG=![]() (∠AEF+∠BEG)=
(∠AEF+∠BEG)=![]() (∠AEB-∠FEG).
(∠AEB-∠FEG).
∴∠AEN +∠BEM=![]() (180°-∠FEG)①,
(180°-∠FEG)①,
又![]() ,
,![]() ,
,
∴两式相加得∠AEN+∠BEM=2∠FEG+30°②,
由①②可得,![]() (180°-∠FEG)=2∠FEG+30°,解得∠FEG=24°,
(180°-∠FEG)=2∠FEG+30°,解得∠FEG=24°,
∴∠AEN+∠BEM =![]() (180°-24°)=78°,
(180°-24°)=78°,
∴∠MEN=180°-(∠AEN+∠BEM) =180°-78°=102°.
故![]() 的度数为24°,
的度数为24°,![]() 的度数为102°.
的度数为102°.
(3)如图3,若点G在点F的左侧,∠FEG=α.
根据(2)知,∠MEN=180°-(AEN+∠BEM)=180°-![]() (∠AEF+∠BEG)=180°-
(∠AEF+∠BEG)=180°-![]() (180°+∠FEG)=90°-
(180°+∠FEG)=90°-![]() ∠FEG.
∠FEG.
∴∠MEN=90°-![]() α.
α.


科目:初中数学 来源: 题型:
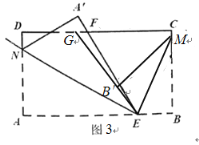
【题目】如图,在平面直角坐标系中,经过点A的双曲线![]() 同时经过点B,且点A在点B的左侧,点A的横坐标为
同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则
,∠AOB=∠OBA=45°,则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
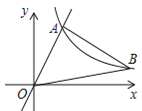
【题目】如图,有一块Rt△ABC的纸片,∠ABC=900,AB=6,BC=8,将△ABC沿AD折叠,使点B落在AC上的E处,则BD的长为( )
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( )
分数 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
人数 | 2 | 4 | 3 | 8 | 10 | 9 | 6 | 3 | 1 |
A. 该组数据的众数是24分
B. 该组数据的平均数是25分
C. 该组数据的中位数是24分
D. 该组数据的极差是8分
查看答案和解析>>
科目:初中数学 来源: 题型:
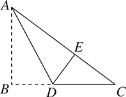
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2018的坐标为_____.
,0),B(0,2),则点B2018的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,
,![]() 是多项式
是多项式![]() 的一次项系数,
的一次项系数,![]() 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式![]() 的次数为
的次数为![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若将数轴在点![]() 处折叠,则点
处折叠,则点![]() 与点
与点![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,![]() 秒钟过后,若点
秒钟过后,若点![]() 与点B之间的距离表示为
与点B之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() = ,
= , ![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(4)请问:AB+BC的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
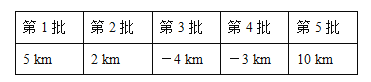
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com