练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，有一块Rt△ABC的纸片，∠ABC=900,AB＝6，BC＝8，将△ABC沿AD折叠，使点B落在AC上的E处，则BD的长为( )

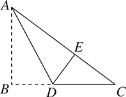
    A.3B.4C.5D.6

    【答案】A

    【解析】

    由题意可得∠AED=∠ABC =90°，AE=AB=3，由勾股定理即可求得AC的长，则可得EC的长，然后设BD=ED=x，则CD=BCBD=4x，由勾股定理CD =EC+ED，即可得方程，解方程即可求得答案．

    ∵点E是沿AD折叠，点B的对应点，连接ED，

    ∴∠AED=∠ABC=90°，AE=AB=6，

    ∵在Rt△ABC中，∠B=90°，AB=6，BC=8，

    ∴AC= =10，

    ∴EC=ACAE=106=4，

    设BD=ED=x，则CD=BCBD=8x，

    在Rt△CDE中，CD=EC+ED，

    即：(8x) =x+16，

    解得：x=3，

    ∴BD=3．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】操作探究：已知在纸面上有一数轴(如图所示).

    左右折叠纸面，折痕所在的直线与数轴的交点为“对折中心点”

    操作一：

    (1)左右折叠纸面，使1表示的点与-1表示的点重合，则-3表示的点与 表示的点重合；

    操作二：

    (2)左右折叠纸面，使-1表示的点与3表示的点重合，回答以下问题：

    ①对折中心点所表示的数为 ,对折后5表示的点与数 表示的点重合；

    ②若数轴上A.B两点之间距离为11（A在B的左侧），且A.B两点经折叠后重合，求A.B两点表示的数是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某蔬菜加工公司先后两批收购蒜苔（tái）共100吨，第一批蒜苔价格为1万元/吨；因蒜苔大量上市，第二批价格跌至0.4万元/吨，这两批蒜苔共用去52万元．

    （1）求两批各购进蒜苔多少吨？

    （2）公司收购后对蒜苔进行加工，分为粗加工和精加工两种．粗加工每吨利润400元，精加工每吨利润1600元要求精加工数量不大于粗加工数量的三倍．为获得最大利润，精加工数量应为多少吨？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线，垂足分别为E、F，连接BF、CE.

    (1)求证：四边形BECF是平行四边形；

    (2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

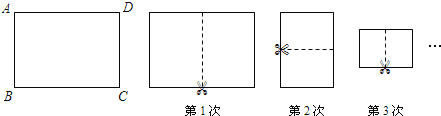
    【题目】将一张长与宽之比为的矩形纸片ABCD进行如下操作：对折并沿折痕剪开，发现每一次所得到的两个矩形纸片长与宽之比都是（每一次的折痕如下图中的虚线所示）．已知AB=1，则第3次操作后所得到的其中一个矩形纸片的周长是 ；第2016次操作后所得到的其中一个矩形纸片的周长是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

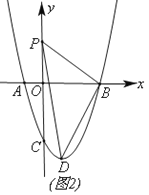
    【题目】如图,在平面直角坐标中，抛物线y=ax2－2ax－3a(a≠0)与x轴交于A、B(A在B的左侧)，与y轴交于点C,且OC=3OA.

    （1）如图（1）求抛物线的解析式；

    （2）如图（2）动点P从点O出发，沿y轴正方向以每秒1个单位的速度移动，点D是抛物线顶点，连接PB、PD、BD，设点P运动时间为t（单位：秒），△PBD的面积为S，求S与t的函数关系式；

    （3）如图（3）在（2）的条件下，延长BP交抛物线于点Q，过点O作OE⊥BQ，垂足为E，连接CE、CB，若CE=CB，求t值，并求出此时的Q点坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是

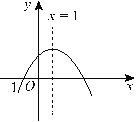
    A．a＞0

    B．当-1＜x＜3时，y＞0

    C．c＜0

    D．当x≥1时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知长方形纸片，点在边上，点在边上，将沿翻折到，射线与交于点.点在边上，将沿翻折到，射线与交于点.

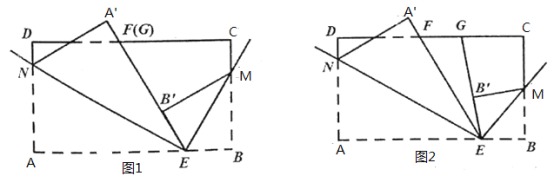
    （1）如图1，若点与点重合，直接写出以为顶点的两对相等的角，并求的度数；

    （2）如图2，若点在点的右侧，且，，求与的度数；

    （3）若点在点的左侧，且，求的度数（用含的代数式表示）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在解决问题：已知a=，求2a2﹣8a+1的值，他是这样分析与解的：

    ∵a===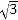2﹣

    ∴a﹣2=﹣

    ∴（a﹣2）2=3，a2﹣4a+4=3

    ∴a2﹣4a=﹣1

    ∴2a2﹣8a+1=2（a2﹣4a）+1=2×（﹣1）+1=﹣1

    请你根据小明的分析过程，解决如下问题：

    （1）化简+++…+

    （2）若a=，求4a2﹣8a+1的值．

    查看答案和解析>>

    同步练习册答案