练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是

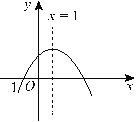
    A．a＞0

    B．当-1＜x＜3时，y＞0

    C．c＜0

    D．当x≥1时，y随x的增大而增大

    【答案】B.

    【解析】

    试题分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

    A、抛物线的开口方向向下，则a＜0．故本选项错误；

    B、根据图示知，抛物线的对称轴为x=1，抛物线与x轴的一交点的横坐标是-1，则抛物线与x轴的另一交点的横坐标是3，

    所以当-1＜x＜3时，y＞0．故本选项正确；

    C、根据图示知，该抛物线与y轴交与正半轴，则c＞0．故本选项错误；

    D、根据图示知，当x≥1时，y随x的增大而减小，故本选项错误．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算题

    （1）

    （2）

    （3）

    （4）

    （5）

    （6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，P为CD中点，点Q为AB上的动点（不与A，B重合）．过Q作QM⊥PA于M，QN⊥PB于N．设AQ的长度为x，QM与QN的长度和为y．则能表示y与x之间的函数关系的图象大致是（　）

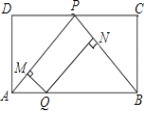
    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有一块Rt△ABC的纸片，∠ABC=900,AB＝6，BC＝8，将△ABC沿AD折叠，使点B落在AC上的E处，则BD的长为( )

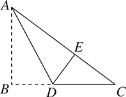
    A.3B.4C.5D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．

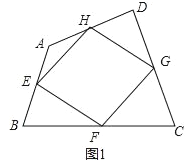
    （1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；

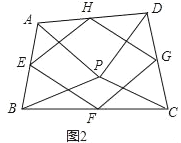
    （2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；

    （3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读第①小题的计算方法，再计算第②小题．

    ①–5+（–9）+17+（–3）

    解：原式=[（–5）+（–）]+[（–9）+（–）]+（17+）+[（–3+（–）]

    =[（–5）+（–9）+（–3）+17]+[（–）+（–）+（–）+]

    =0+（–1）

    =–1．

    上述这种方法叫做拆项法．灵活运用加法的交换律、结合律可使运算简便．

    ②仿照上面的方法计算：（﹣2000）+（﹣1999）+4000+（﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学将某班级毕业升学体育测试成绩（满分30分）统计整理，得到下表，则下列说法错误的是（　　）

    分数

    20

    21

    22

    23

    24

    25

    26

    27

    28

    人数

    2

    4

    3

    8

    10

    9

    6

    3

    1

    A. 该组数据的众数是24分

    B. 该组数据的平均数是25分

    C. 该组数据的中位数是24分

    D. 该组数据的极差是8分

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（，0），B（0，2），则点B2018的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

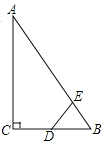
    【题目】如图，Rt△ABC中，，，，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿AB向B点运动，设E点的运动时间为t秒，连接DE，当以B、D、E为顶点的三角形与△ABC相似时，t的值为（　　）

    A.2或3.5B.2或3.2C.2或3.4D.3.2或3.4

    查看答案和解析>>

    同步练习册答案