
°æƒø°øŒ“√«∏¯≥ˆ»Áœ¬∂®“£∫À≥¥Œ¡¨Ω”»Œ“‚“ª∏ˆÀƒ±þ–Œ∏˜±þ÷–µ„À˘µ√µƒÀƒ±þ–ŒΩ–÷–µ„Àƒ±þ–Œ£Æ
£®1£©»ÁÕº1£¨Àƒ±þ–ŒABCD÷–£¨µ„E£¨F£¨G£¨H∑÷±Œ™±þAB£¨BC£¨CD£¨DAµƒ÷–µ„£Æ«Û÷§£∫÷–µ„Àƒ±þ–ŒEFGH «∆Ω––Àƒ±þ–Œ£ª
£®2£©»ÁÕº2£¨µ„P «Àƒ±þ–ŒABCDƒ⁄“ªµ„£¨«“¬˙◊„PA=PB£¨PC=PD£¨°œAPB=°œCPD£¨µ„E£¨F£¨G£¨H∑÷±Œ™±þAB£¨BC£¨CD£¨DAµƒ÷–µ„£¨≤¬œÎ÷–µ„Àƒ±þ–ŒEFGHµƒ–Œ◊¥£¨≤¢÷§√˜ƒ„µƒ≤¬œÎ£ª
£®3£©»Ù∏ƒ±‰£®2£©÷–µƒÃıº˛£¨ π°œAPB=°œCPD=90°„£¨∆‰À˚Ãıº˛≤ª±‰£¨÷±Ω”–¥≥ˆ÷–µ„Àƒ±þ–ŒEFGHµƒ–Œ◊¥£¨≤¢÷§√˜ƒ„µƒ≤¬œÎ£Æ
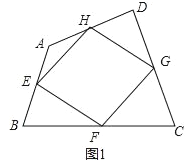
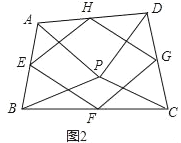
°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©Àƒ±þ–ŒEFGH «¡‚–Œ£ª£®3£©Àƒ±þ–ŒEFGH «’˝∑Ω–Œ.
°æΩ‚Œˆ°ø∑÷Œˆ£∫£®1£©»ÁÕº1÷–£¨¡¨Ω”BD£¨∏˘æð»˝Ω«–Œ÷–Œªœþ∂®¿Ì÷ª“™÷§√˜EH°ŒFG£¨EH=FGº¥ø…£Æ
£®2£©Àƒ±þ–ŒEFGH «¡‚–Œ£Æœ»÷§√˜°˜APC°’°˜BPD£¨µ√µΩAC=BD£¨‘Ÿ÷§√˜EF=FGº¥ø…£Æ
£®3£©Àƒ±þ–ŒEFGH «’˝∑Ω–Œ£¨÷ª“™÷§√˜°œEHG=90°„£¨¿˚”√°˜APC°’°˜BPD£¨µ√°œACP=°œBDP£¨º¥ø…÷§√˜°œCOD=°œCPD=90°„£¨‘Ÿ∏˘æð∆Ω––œþµƒ–‘÷ º¥ø…÷§√˜£Æ
œÍΩ‚£∫£®1£©»ÁÕº1£¨¡¨Ω”BD£¨
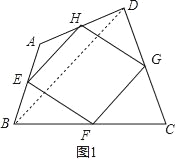
°þµ„E°¢H∑÷±Œ™±þAB°¢ADµƒ÷–µ„£¨
°ýEH°ŒBD°¢EH=![]() BD£¨
BD£¨
°þµ„F°¢G∑÷±Œ™BC°¢DCµƒ÷–µ„£¨
°ýFG°ŒBD°¢FG=![]() BD£¨
BD£¨
°ýEH=FG°¢EH°ŒFG£¨
°ý÷–µ„Àƒ±þ–ŒEFGH «∆Ω––Àƒ±þ–Œ£ª
£®2£©Àƒ±þ–ŒEFGH «¡‚–Œ£¨
»ÁÕº2£¨¡¨Ω”AC°¢BD£¨
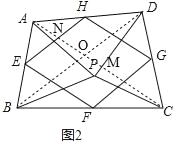
°þ°œAPB=°œCPD£¨
°ý°œAPB+°œAPD=°œCPD+°œAPD£¨º¥°œAPC=°œBPD£¨
‘⁄°˜APC∫Õ°˜BPD÷–£¨
AP=BP£¨°œAPC=°œBPD£¨PC=PD£¨
°ý°˜APC°’°˜BPD£®SAS£©£¨
°ýAC=BD£¨
°þµ„E°¢F°¢G∑÷±Œ™AB°¢BC°¢CDµƒ÷–µ„£¨
°ýEF=![]() AC°¢FG=
AC°¢FG=![]() BD£¨
BD£¨
°ýEF=FG£¨
°þÀƒ±þ–ŒEFGH «∆Ω––Àƒ±þ–Œ£¨
°ýÀƒ±þ–ŒEFGH «¡‚–Œ£ª
£®3£©Àƒ±þ–ŒEFGH «’˝∑Ω–Œ£¨
…ËAC°¢BDΩªµ„Œ™O£¨AC”ÎPDΩª”⁄µ„M£¨AC”ÎEHΩª”⁄µ„N£¨
°þ°˜APC°’°˜BPD£¨
°ý°œACP=°œBDP£¨
°þ°œDMO=°œCMP£¨
°ý°œCOD=°œCPD=90°„£¨
°þEH°ŒBD°¢AC°ŒHG£¨
°ý°œEHG=°œENO=°œBOC=°œDOC=90°„£¨
°þÀƒ±þ–ŒEFGH «¡‚–Œ£¨
°ýÀƒ±þ–ŒEFGH «’˝∑Ω–Œ£Æ


 –°—ßøŒÃ√◊˜“µœµ¡–¥∞∏
–°—ßøŒÃ√◊˜“µœµ¡–¥∞∏ Ω≤© ø“ªµ„»´Õ®œµ¡–¥∞∏
Ω≤© ø“ªµ„»´Õ®œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() «
«![]() µƒΩ«∆Ω∑÷œþ£¨
µƒΩ«∆Ω∑÷œþ£¨![]() °¢
°¢![]() ∑÷± «±þ
∑÷± «±þ![]() °¢
°¢![]() µƒ÷–µ„£¨¡¨Ω”
µƒ÷–µ„£¨¡¨Ω”![]() °¢
°¢![]() £¨‘⁄≤ª‘Ÿ¡¨Ω”∆‰À˚œþ∂Œµƒ«∞÷œ¬£¨“™ πÀƒ±þ–Œ
£¨‘⁄≤ª‘Ÿ¡¨Ω”∆‰À˚œþ∂Œµƒ«∞÷œ¬£¨“™ πÀƒ±þ–Œ![]() ≥…Œ™¡‚–Œ£¨ªπ–ËÃ̺”“ª∏ˆÃıº˛£¨’‚∏ˆÃıº˛≤ªø…ƒÐ «£® £©
≥…Œ™¡‚–Œ£¨ªπ–ËÃ̺”“ª∏ˆÃıº˛£¨’‚∏ˆÃıº˛≤ªø…ƒÐ «£® £©
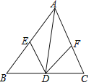
A. BD=DC B. AB=AC
C. AD=BC D. AD°ÕBC
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡≤ƒ¡œ£∫
–°√˜‘⁄—ßœ∞∂˛¥Œ∏˘ Ω∫Û£¨∑¢œ÷“ª–©∫¨∏˘∫≈µƒ Ω◊”ø…“‘–¥≥…¡Ì“ª∏ˆ Ω◊”µƒ∆Ω∑Ω£¨»Á![]() £Æ…∆”⁄Àºøºµƒ–°√˜Ω¯––¡À“‘œ¬ÃΩÀ˜£∫
£Æ…∆”⁄Àºøºµƒ–°√˜Ω¯––¡À“‘œ¬ÃΩÀ˜£∫
…Ë![]() £®∆‰÷–
£®∆‰÷–![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() æ˘Œ™’˚ ˝£©£¨‘Ú”–
æ˘Œ™’˚ ˝£©£¨‘Ú”–![]() £Æ
£Æ
![]() £¨
£¨![]() £Æ’‚—˘–°√˜æÕ’“µΩ¡À“ª÷÷∞—¿ýÀ∆
£Æ’‚—˘–°√˜æÕ’“µΩ¡À“ª÷÷∞—¿ýÀ∆![]() µƒ Ω◊”ªØŒ™∆Ω∑Ω Ωµƒ∑Ω∑®£Æ
µƒ Ω◊”ªØŒ™∆Ω∑Ω Ωµƒ∑Ω∑®£Æ
«Îƒ„∑¬’’–°√˜µƒ∑Ω∑®ÃΩÀ˜≤¢Ω‚戜¬¡–Œ £∫
£®1£©µ±![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() æ˘Œ™’˝’˚ ˝ ±£¨»Ù
æ˘Œ™’˝’˚ ˝ ±£¨»Ù![]() £¨”√∫¨
£¨”√∫¨![]() °¢
°¢![]() µƒ Ω◊”∑÷±±Ì æ
µƒ Ω◊”∑÷±±Ì æ![]() °¢
°¢![]() £¨µ√£∫
£¨µ√£∫![]() °°°°£¨
°°°°£¨![]() °°°°£ª
°°°°£ª
£®2£©¿˚”√À˘ÃΩÀ˜µƒΩ·¬€£¨’““ª◊È’˝’˚ ˝![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() ÃÓø’£∫°°°°
ÃÓø’£∫°°°°![]() °°°°
°°°°![]() °°°°
°°°°![]() °°°°
°°°°![]()
![]() £ª
£ª
£®3£©»Ù![]() £¨«“
£¨«“![]() °¢
°¢![]() °¢
°¢![]() æ˘Œ™’˝’˚ ˝£¨«Û
æ˘Œ™’˝’˚ ˝£¨«Û![]() µƒ÷µ£ø
µƒ÷µ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
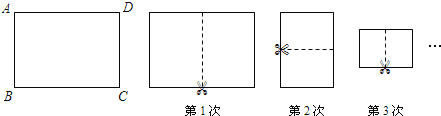
°æƒø°øΩ´“ª’≈≥§”ÎøÌ÷Ʊ»Œ™![]() µƒæÿ–Œ÷Ω∆¨ABCDΩ¯––»Áœ¬≤Ÿ◊˜£∫∂‘’€≤¢—ÿ’€∫€ºÙø™£¨∑¢œ÷√ø“ª¥ŒÀ˘µ√µΩµƒ¡Ω∏ˆæÿ–Œ÷Ω∆¨≥§”ÎøÌ÷Ʊ»∂º «
µƒæÿ–Œ÷Ω∆¨ABCDΩ¯––»Áœ¬≤Ÿ◊˜£∫∂‘’€≤¢—ÿ’€∫€ºÙø™£¨∑¢œ÷√ø“ª¥ŒÀ˘µ√µΩµƒ¡Ω∏ˆæÿ–Œ÷Ω∆¨≥§”ÎøÌ÷Ʊ»∂º «![]() £®√ø“ª¥Œµƒ’€∫€»Áœ¬Õº÷–µƒ–ÈœþÀ˘ 棩£Æ“—÷™AB=1£¨‘Úµ⁄3¥Œ≤Ÿ◊˜∫ÛÀ˘µ√µΩµƒ∆‰÷–“ª∏ˆæÿ–Œ÷Ω∆¨µƒ÷Ð≥§ « £ªµ⁄2016¥Œ≤Ÿ◊˜∫ÛÀ˘µ√µΩµƒ∆‰÷–“ª∏ˆæÿ–Œ÷Ω∆¨µƒ÷Ð≥§ « £Æ
£®√ø“ª¥Œµƒ’€∫€»Áœ¬Õº÷–µƒ–ÈœþÀ˘ 棩£Æ“—÷™AB=1£¨‘Úµ⁄3¥Œ≤Ÿ◊˜∫ÛÀ˘µ√µΩµƒ∆‰÷–“ª∏ˆæÿ–Œ÷Ω∆¨µƒ÷Ð≥§ « £ªµ⁄2016¥Œ≤Ÿ◊˜∫ÛÀ˘µ√µΩµƒ∆‰÷–“ª∏ˆæÿ–Œ÷Ω∆¨µƒ÷Ð≥§ « £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø”√°∞°±πÊ∂®“ª÷÷–¬‘ÀÀ„£∫∂‘”⁄»Œ“‚”–¿Ì ˝a∫Õb£¨πÊ∂®ab£Ωab+2ab+a£Æ »Á£∫13£Ω1°¡3+2°¡1°¡3+1£Ω16
£®1£©«Û3£®©Å1£©µƒ÷µ£ª
£®2£©»Ù£®a+1£©2£Ω36£¨«Ûaµƒ÷µ£ª
£®3£©»Ùm£Ω2x£¨n£Ω£®![]() x£©3£®∆‰÷–xŒ™”–¿Ì ˝£©£¨ ‘±»Ωœm°¢nµƒ¥Û–°£Æ
x£©3£®∆‰÷–xŒ™”–¿Ì ˝£©£¨ ‘±»Ωœm°¢nµƒ¥Û–°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂˛¥Œ∫Ø ˝y=ax2+bx+c£®a°Ÿ0£©µƒÕºœÛ»ÁÕºÀ˘ 棨‘Úœ¬¡–Ω·¬€÷–’˝»∑µƒ «
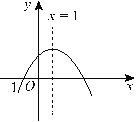
A£Æa£æ0
B£Æµ±-1£ºx£º3 ±£¨y£æ0
C£Æc£º0
D£Æµ±x°ð1 ±£¨yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥µÁ–≈π´Àæ”–A°¢B¡Ω÷÷º∆∑—∑Ω∞∏£∫‘¬Õ®ª∞∑—”√y£®‘™£©”ÎÕ®ª∞ ±º‰x£®∑÷÷”£©µƒπÿœµ£¨»ÁÕºÀ˘ 棨œ¬¡–Àµ∑®÷–’˝»∑µƒ «£®°°°°£©
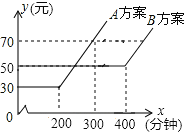
A.‘¬Õ®ª∞ ±º‰µÕ”⁄200∑÷÷”—°B∑Ω∞∏ªÆÀ„
B.‘¬Õ®ª∞ ±º‰≥¨π˝300∑÷÷”«“…Ÿ”⁄400∑÷÷”—°A∑Ω∞∏ªÆÀ„
C.‘¬Õ®ª∞∑—”√Œ™70‘™ ±£¨A∑Ω∞∏±»B∑Ω∞∏µƒÕ®ª∞ ±º‰≥§
D.‘¬Õ®ª∞ ±º‰‘⁄400∑÷÷”ƒ⁄£¨B∑Ω∞∏Õ®ª∞∑—”√ º÷’ «50‘™
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº:‘⁄ ˝÷·…œµ„![]() ±Ì æ ˝
±Ì æ ˝![]() £¨µ„
£¨µ„![]() ±Ì æ ˝
±Ì æ ˝![]() £¨µ„
£¨µ„![]() ±Ì æ ˝
±Ì æ ˝![]() £¨
£¨![]() «∂ýœÓ Ω
«∂ýœÓ Ω![]() µƒ“ª¥ŒœÓœµ ˝£¨
µƒ“ª¥ŒœÓœµ ˝£¨![]() «æ¯∂‘÷µ◊Ó–°µƒ’˚ ˝£¨µ•œÓ Ω
«æ¯∂‘÷µ◊Ó–°µƒ’˚ ˝£¨µ•œÓ Ω![]() µƒ¥Œ ˝Œ™
µƒ¥Œ ˝Œ™![]() .
.
![]()
£®1£©![]() = £¨
= £¨![]() = £¨
= £¨![]() = ;
= ;
£®2£©»ÙΩ´ ˝÷·‘⁄µ„![]() ¥¶’€µ˛£¨‘Úµ„
¥¶’€µ˛£¨‘Úµ„![]() ”ε„
”ε„![]() ÷ÿ∫œ( ÃÓ°∞ƒÐ°±ªÚ°∞≤ªƒÐ°±)£ª
÷ÿ∫œ( ÃÓ°∞ƒÐ°±ªÚ°∞≤ªƒÐ°±)£ª
£®3£©µ„![]() ø™ º‘⁄ ˝÷·…œ‘À∂Ø£¨»Ùµ„
ø™ º‘⁄ ˝÷·…œ‘À∂Ø£¨»Ùµ„![]() “‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ”“‘À∂Ø£¨Õ¨ ±,µ„
“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ”“‘À∂Ø£¨Õ¨ ±,µ„![]() ∫Õµ„
∫Õµ„![]() ∑÷±“‘√ø√Î3∏ˆµ•Œª≥§∂»∫Õ2∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ◊Û‘À∂Ø£¨
∑÷±“‘√ø√Î3∏ˆµ•Œª≥§∂»∫Õ2∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ◊Û‘À∂Ø£¨![]() √Î÷”π˝∫Û£¨»Ùµ„
√Î÷”π˝∫Û£¨»Ùµ„![]() ”ε„B÷ƺ‰µƒæý¿Î±Ì 挙
”ε„B÷ƺ‰µƒæý¿Î±Ì 挙![]() £¨µ„
£¨µ„![]() ”ε„
”ε„![]() ÷ƺ‰µƒæý¿Î±Ì 挙
÷ƺ‰µƒæý¿Î±Ì 挙![]() £¨‘Ú
£¨‘Ú![]() = ,
= , ![]() = (”√∫¨
= (”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ);
µƒ¥˙ ˝ Ω±Ì æ);
£®4£©«ÎŒ £∫AB+BCµƒ÷µ «∑ÒÀÊ◊≈ ±º‰![]() µƒ±‰ªØ∂¯∏ƒ±‰£ø»Ù±‰ªØ£¨«ÎÀµ√˜¿Ì”…£ª»Ù≤ª±‰£¨«Î«Û∆‰÷µ.
µƒ±‰ªØ∂¯∏ƒ±‰£ø»Ù±‰ªØ£¨«ÎÀµ√˜¿Ì”…£ª»Ù≤ª±‰£¨«Î«Û∆‰÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…õ͜˙ €10îA–Õ∫Õ20îB–ÕµÁƒ‘µƒ¿˚»ÛŒ™4000‘™£¨œ˙ €20îA–Õ∫Õ10îB–ÕµÁƒ‘µƒ¿˚»ÛŒ™3500‘™.
£®1£©«Û√øîA–ÕµÁƒ‘∫ÕB–ÕµÁƒ‘µƒœ˙ €¿˚»Û£ª
£®2£©∏√…õͺ∆ªÆ“ª¥Œπ∫Ω¯¡Ω÷÷–Õ∫≈µƒµÁƒ‘π≤100∆‰÷–B–ÕµÁƒ‘µƒΩ¯ªı¡ø≤ª≥¨π˝A–ÕµÁƒ‘µƒ2±∂£¨…Ëπ∫Ω¯A–ÕµÁƒ‘x’‚100îµÁƒ‘µƒœ˙ €◊п˚»ÛŒ™y‘™.
¢Ÿ«Ûyπÿ”⁄xµƒ∫Ø ˝πÿœµ Ω£ª
¢⁄∏√…õÍπ∫Ω¯A–Õ°¢B–ÕµÁƒ‘∏˜∂ý…ŸÃ®£¨≤≈ƒÐ πœ˙ €◊п˚»Û◊Ó¥Û£ø
£®3£© µº Ω¯ªı ±£¨≥ߺ“∂‘A–ÕµÁƒ‘≥ˆ≥ߺ€œ¬µ˜m(0<m<100)‘™£¨«“œÞ∂®…õÍ◊Ó∂ýπ∫Ω¯A–ÕµÁƒ‘70î.»Ù…õͱ£≥÷¡Ω÷÷µÁƒ‘µƒ €º€≤ª±‰£¨«Îƒ„∏˘æð“‘…œ–≈œ¢º∞(2)÷–Ãıº˛£¨…˺∆≥ˆ π’‚100îµÁƒ‘œ˙ €◊п˚»Û◊Ó¥ÛµƒΩ¯ªı∑Ω∞∏.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com