
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,
,![]() 是多项式
是多项式![]() 的一次项系数,
的一次项系数,![]() 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式![]() 的次数为
的次数为![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若将数轴在点![]() 处折叠,则点
处折叠,则点![]() 与点
与点![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,![]() 秒钟过后,若点
秒钟过后,若点![]() 与点B之间的距离表示为
与点B之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() = ,
= , ![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(4)请问:AB+BC的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1)a= -4 ,b= 0,c=6;(2)不能 ;(3)B=t+4,BC= 3t + 6;(4)AB+BC的值是随着时间t的变化而改变.
【解析】
(1)根据多项式与单项式的概念即可求出答案;
(2)根据a、b、c的值确定A、C是否关于点B对称即可;
(3)根据A、B、C三点的运动速度和运动方向可得;
(4)将(3)中的AB与BC的表达式代入即可判断.
(1)∵多项式![]() 的一次项系数为-4,绝对值最小的整数是0,单项式
的一次项系数为-4,绝对值最小的整数是0,单项式![]() 的次数为6,
的次数为6,
∴a=-4,b=0,c=6;
(2)不能重合,由-4和6的中点为1,故将数轴在点B出折叠,点A和点C不能重合;
(3)由于点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,
∴![]() 秒钟过后,AB=3t+4-2t=t+4;
秒钟过后,AB=3t+4-2t=t+4;
由于点![]() 以每秒1个单位长度的速度向右运动,
以每秒1个单位长度的速度向右运动,
∴![]() 秒钟过后,BC=2t+6+t=3t+6;
秒钟过后,BC=2t+6+t=3t+6;
(4)AB+BC=(t+4)+(3t+6)=4t+10,
所以,AB+BC的值是随着时间t的变化而改变.


科目:初中数学 来源: 题型:
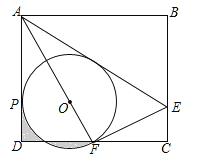
【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④
CE;④![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
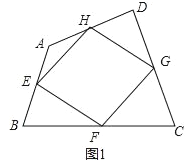
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
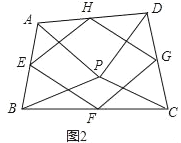
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( )
分数 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
人数 | 2 | 4 | 3 | 8 | 10 | 9 | 6 | 3 | 1 |
A. 该组数据的众数是24分
B. 该组数据的平均数是25分
C. 该组数据的中位数是24分
D. 该组数据的极差是8分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,请回答下列问题.

(1)A、B、C三点分别表示 、 、 ;
(2)将点B向左移动3个单位长度后,点B所表示的数是 ;
(3)将点A向右移动4个单位长度后,点A所表示的数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2018的坐标为_____.
,0),B(0,2),则点B2018的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(m+1)x+m2﹣3=0.
(1)当m取何值时,方程有两个不相等的实数根?
(2)设x1、x2是方程的两根,且x12+x22=22+x1x2,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7 月 9 日,滴滴发布北京市滴滴网约车价格调整,公布了新的滴滴快车计价规则,车费由“总里程费+总时长费”两部分构成,不同时段收费标准不同,具体收费标准如下表,如果车费不足起步价,则按起步价收费.
时间段 | 里程费(元/千米) | 时长费(元/分钟) | 起步价(元) |
06:00-10:00 | 1.80 | 0.80 | 14.00 |
10:00-17:00 | 1.45 | 0.40 | 13.00 |
17:00-21:00 | 1.50 | 0.80 | 14.00 |
21:00-6:00 | 2.15 | 0.80 | 14.00 |
(1)小明早上 7:10 乘坐滴滴快车上学,行车里程 6 千米,行车时间 10 分钟,则应付车费多少元?
(2)小云 17:10 放学回家,行车里程 1 千米,行车时间 15 分钟,则应付车费多少元?
(3)下晚自习后小明乘坐滴滴快车回家,20:45 在学校上车,由于堵车,平均速度是 a 千米/小时,15 分钟后走另外一条路回家,平均速度是 b 千米/小时,5 分钟后到家,则他应付车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
八年级:
76 88 93 65 78 94 89 68 95 50 89 88 89 89 77 94 87 88 92 91
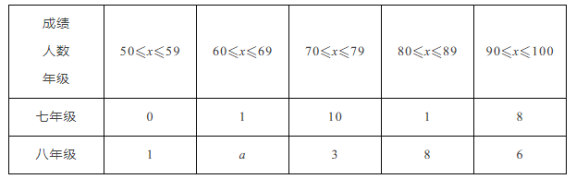
平均数、中位数、众数如表所示:
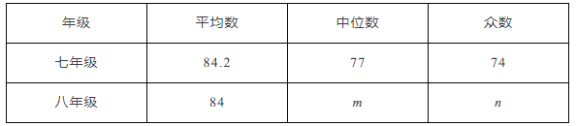
根据以上信息,回答下列问题:
(1)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)该校对读书知识竞赛成绩不少于80分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有______人;
(3)结合以上数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com