
【题目】已知关于x的方程x2﹣2(m+1)x+m2﹣3=0.
(1)当m取何值时,方程有两个不相等的实数根?
(2)设x1、x2是方程的两根,且x12+x22=22+x1x2,求实数m的值.
【答案】(1)m>﹣2;(2)实数m的值为1.
【解析】分析:
(1)根据“一元二次方程![]() 中,当根的判别式△=
中,当根的判别式△=![]() 时,方程有两个不相等的实数根”列出不等式进行解答即可;
时,方程有两个不相等的实数根”列出不等式进行解答即可;
(2)根据“一元二次方程根与系数的关系”可得![]() ,将所得等式代入x12+x22=22+x1x2中得到关于m的方程,并结合(1)中所得m的取值范围即可求得m的值.
,将所得等式代入x12+x22=22+x1x2中得到关于m的方程,并结合(1)中所得m的取值范围即可求得m的值.
详解:
(1)由题意可得:在关于x的方程x2﹣2(m+1)x+m2﹣3=0中,
△=[﹣2(m+1)]2﹣4(m2﹣3)=8m+16,
∵关于x的方程x2﹣2(m+1)x+m2﹣3=0有两个不相等的实数根时,
∴△>0,即8m+16>0,解得m>﹣2;
(2)根据一元二次方程根与系数之间的关系,
得x1+x2=2(m+1),x1x2=m2﹣3,
∵x12+x22=22+x1x2=(x1+x2)2﹣2x1x2,
∴[2(m+1)]﹣2(m2﹣3)=6+(m2﹣3),
化简,得m2+8m﹣9=0,解得m=1或m=﹣9(不合题意,舍去),
∴实数m的值为1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得:
,得:![]() ,
,![]() ;
;
(2)利用所探索的结论,找一组正整数![]() 、
、![]() 、
、![]() 、
、![]() 填空:
填空: ![]()
![]()
![]()
![]()
![]() ;
;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司有A、B两种计费方案:月通话费用y(元)与通话时间x(分钟)的关系,如图所示,下列说法中正确的是( )
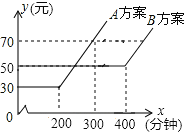
A.月通话时间低于200分钟选B方案划算
B.月通话时间超过300分钟且少于400分钟选A方案划算
C.月通话费用为70元时,A方案比B方案的通话时间长
D.月通话时间在400分钟内,B方案通话费用始终是50元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,
,![]() 是多项式
是多项式![]() 的一次项系数,
的一次项系数,![]() 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式![]() 的次数为
的次数为![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若将数轴在点![]() 处折叠,则点
处折叠,则点![]() 与点
与点![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,![]() 秒钟过后,若点
秒钟过后,若点![]() 与点B之间的距离表示为
与点B之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() = ,
= , ![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(4)请问:AB+BC的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人.
(1)求第一轮后患病的人数;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在数轴上表示下列各数,并用“<”号把它们连接.
3, -1, 0, -2.5, 1.5, 2![]()
(2)快递员要从物流中心出发送货,已知甲住户在物流中心的东边 2km 处,乙住户在甲住户的西边 3km 处,丙住户在物流中心的西边 1.5km 处,请建立数轴表示物流中心、甲住户、乙住户、丙住户的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,E是BC上一点,F是CD延长线上一点,![]() ,连接AE,AF,EF,G为EF中点,连接AG,DG.
,连接AE,AF,EF,G为EF中点,连接AG,DG.

(1)如图1:若![]() ,
,![]() ,求DG;
,求DG;
(2)如图2:延长GD至M,使![]() ,过M作MN∥FD交AF的延长线于N,连接NG,若
,过M作MN∥FD交AF的延长线于N,连接NG,若![]() .求证:
.求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com