
【题目】正方形ABCD中,E是BC上一点,F是CD延长线上一点,![]() ,连接AE,AF,EF,G为EF中点,连接AG,DG.
,连接AE,AF,EF,G为EF中点,连接AG,DG.

(1)如图1:若![]() ,
,![]() ,求DG;
,求DG;
(2)如图2:延长GD至M,使![]() ,过M作MN∥FD交AF的延长线于N,连接NG,若
,过M作MN∥FD交AF的延长线于N,连接NG,若![]() .求证:
.求证:![]() .
.
【答案】(1)DG=![]() ;(2)
;(2)![]() ,见解析.
,见解析.
【解析】
(1)取CF的中点H,连接GH;先证明△ABE≌△ADF(SAS),在证明△AEF是等腰直角三角形,由GH是Rt△EFC的中位线,在Rt△DGH中即可求解;
(2)过点G作GK⊥MN,交NM的延长线与点K,交CF于点Q,过点G作GT⊥AF,交AF于点T;设BE=a,分别求出![]() ,
,![]() ,
,![]() ,再由△AFE是等腰直角三角形,G是EF的中点,求出
,再由△AFE是等腰直角三角形,G是EF的中点,求出![]()
![]()
![]() ,证明△NGK≌△NGT(HL),则有TN=NK=MN+MK,∠ANG=30°,可求
,证明△NGK≌△NGT(HL),则有TN=NK=MN+MK,∠ANG=30°,可求![]()
![]()
![]() ,
,![]() 得到
得到![]() =MN+NA.
=MN+NA.
解:(1)取CF的中点H,连接GH,
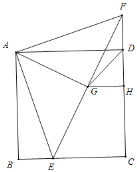
∵BE=DF,AB=AD,∠ADF=∠B=90°,
∴△ABE≌△ADF(SAS),
∴AF=AE,
∵AB=3,BE=1,
∴AF=AE=![]() ,CF=4,CE=2,
,CF=4,CE=2,
∴EF=2![]() ,
,
∴△AEF是等腰直角三角形,
∵G为EF中点,CF的中点H,
∴GH是Rt△EFC的中位线,
∴GH=![]() CE=1,
CE=1,
∴FH=2,
∴DH=1,
∴DG=![]() ;
;
(2)过点G作GK⊥MN,交NM的延长线与点K,交CF于点Q,
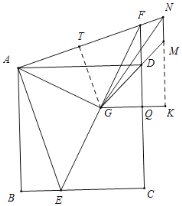
过点G作GT⊥AF,交AF于点T;
设BE=a,
在Rt△ABE中,∠BAE=30°,
∴AB=![]() a,AE=2a,
a,AE=2a,
∴CE=(![]() -1)a,
-1)a,
∵DF=BE,
∴CF=(![]() +1)a,
+1)a,
∵△AFE是等腰直角三角形,G是EF的中点,
∴AG=![]() a,
a,
∵G是EF中点,GQ⊥CF,
∴GQ=![]() CE=
CE=![]() a,
a,
∴DQ=CD-![]() CF=
CF=![]() a,
a,
∴GQ=DQ,
∴∠DGQ=45°,
∴GK=MK,
∴GM=GA,
∴GK=MK=a,
∵∠FAG=45°,
∴GT=a,
∴Rt△NGK≌Rt△NGT(HL),
∴TN=NK=MN+MK,
∠ANG=![]() ∠ANK,
∠ANK,
∵∠BAE=30°,
∴∠NAD=30°,
∴∠ANK=60°,
∴∠ANG=30°,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(m+1)x+m2﹣3=0.
(1)当m取何值时,方程有两个不相等的实数根?
(2)设x1、x2是方程的两根,且x12+x22=22+x1x2,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
八年级:
76 88 93 65 78 94 89 68 95 50 89 88 89 89 77 94 87 88 92 91
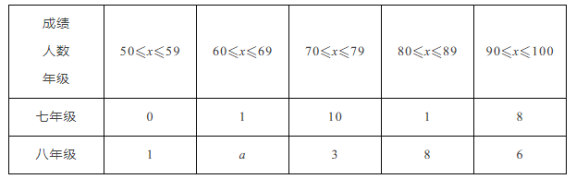
平均数、中位数、众数如表所示:
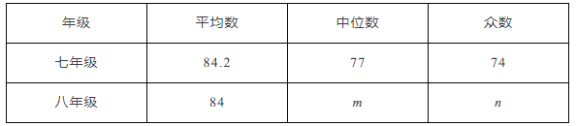
根据以上信息,回答下列问题:
(1)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)该校对读书知识竞赛成绩不少于80分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有______人;
(3)结合以上数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
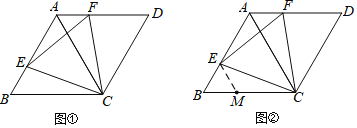
【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD在平面直角坐标系中,A、B(点A在点B的左侧)两点的横坐标是方程![]() 的两个根,点D在y轴上其中
的两个根,点D在y轴上其中![]() .
.

(1)求平行四边形ABCD的面积;
(2)若P是第一象限位于直线BD上方的一点,过P作![]() 于E,过E作
于E,过E作![]() 轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是
轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是![]() ;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求
;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求![]() 的最小值,此时y轴上有一个动点G,当
的最小值,此时y轴上有一个动点G,当![]() 最大时,求G点坐标;
最大时,求G点坐标;
(3)在(2)的情况下,将△AOD绕O点逆时针旋转60°后得到![]() 如图2,将线段
如图2,将线段![]() 沿着x轴平移,记平移过程中的线段
沿着x轴平移,记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点S,使得以点
,在平面直角坐标系中是否存在点S,使得以点![]() ,
,![]() ,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.

(1)求证:四边形AEDF是菱形;
(2)若∠B=30°,BC=4![]() ,求四边形AEDF的周长.
,求四边形AEDF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车一天下午某时间段以广场为出发点,在东西方向的大道上营运,规定向东为正,向西为负,单次行车里程依先后顺序记录如下:(单位:![]() )+9,-3,-5,+4,-8,+7,-2,-5,+8,-4
)+9,-3,-5,+4,-8,+7,-2,-5,+8,-4
(1)该出租车司机将最后一名乘客送到目的地后,出租车在广场的什么方向?距广场多远?
(2)若每千米耗油0.08升,该出租车这个时间段共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图像如图所示。
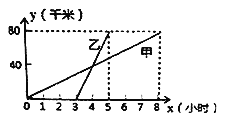
(1)请根据图像回答下列问题:甲先出发 小时后,乙才出发;在甲出发 小时后两人相遇,这时他们距A地 千米;
(2)乙的行驶速度 千米/小时;
(3)分别求出甲、乙在行驶过程中的路程(千米)与时间(小时)之间的函数关系式(不要求写出自变量的取值范围)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com