练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

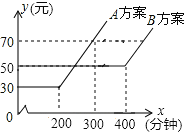
    【题目】某电信公司有A、B两种计费方案：月通话费用y（元）与通话时间x（分钟）的关系，如图所示，下列说法中正确的是（　　）

    A.月通话时间低于200分钟选B方案划算

    B.月通话时间超过300分钟且少于400分钟选A方案划算

    C.月通话费用为70元时，A方案比B方案的通话时间长

    D.月通话时间在400分钟内，B方案通话费用始终是50元

    【答案】D

    【解析】

    根据通话时间少于200分钟时，A、B两方案的费用可判断选项A；根据300＜x＜400时，两函数图象可判断选项B；根据月通话费用为70元时，比较图象的横坐标大小即可判断选项C；根据x≤400，根据图象的纵坐标可判断选项D．

    根据图象可知，当月通话时间低于200分钟时，A方案通话费用始终是30元，B方案通话费用始终是50元，故选项A不合题意；

    当300＜x＜400时，A方案通话费用大于70元，B方案通话费用始终是50元，故选项B不合题意；

    当月通话费用为70元时，A方案通话费时间为300分钟，B方案通话费时间大于400分钟，故选项C不合题意；

    当x≤400时，B方案通话费用始终是50元．故选项D符合题意．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】观察下面一列数，探求其规律：

    （1）请问第7个，第8个，第9个数分别是什么？

    （2）第2007个数是什么？用n的代数式表示这一规律；

    （3）如果这列数无限排列下去，越来越接近哪一个数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=Rt∠，以BC为直径的⊙O交AB于点D，切线DE交AC于点E．

    （1）求证：∠A=∠ADE；

    （2）若AD=16，DE=10，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．

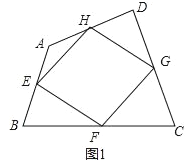
    （1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；

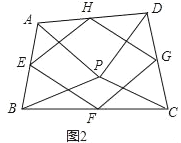
    （2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；

    （3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

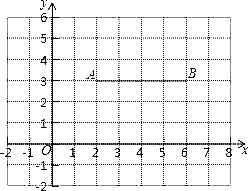
    【题目】如图，在平面直角坐标系中，已知点A（2，3）、B（6，3），连接AB．如果对于平面内一点P，线段AB上都存在点Q，使得PQ≤1，那么称点P是线段AB的“附近点”．

    （1）请判断点D（4.5，2.5）是否是线段AB的“附近点”；

    （2）如果点H （m，n）在一次函数的图象上，且是线段AB的“附近点”，求m的取值范围；

    （3）如果一次函数y=x+b的图象上至少存在一个“附近点”，请直接写出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学将某班级毕业升学体育测试成绩（满分30分）统计整理，得到下表，则下列说法错误的是（　　）

    分数

    20

    21

    22

    23

    24

    25

    26

    27

    28

    人数

    2

    4

    3

    8

    10

    9

    6

    3

    1

    A. 该组数据的众数是24分

    B. 该组数据的平均数是25分

    C. 该组数据的中位数是24分

    D. 该组数据的极差是8分

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上有三个点A、B、C，请回答下列问题．

    （1）A、B、C三点分别表示 、 、 ；

    （2）将点B向左移动3个单位长度后，点B所表示的数是 ；

    （3）将点A向右移动4个单位长度后，点A所表示的数是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2﹣2（m+1）x+m2﹣3=0．

    （1）当m取何值时，方程有两个不相等的实数根？

    （2）设x1、x2是方程的两根，且x12+x22=22+x1x2，求实数m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE＝BD+CE．

    （2）如图（2），将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状并说明理由．

    查看答案和解析>>

    同步练习册答案