
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��2��3����B��6��3��������AB���������ƽ����һ��P���߶�AB�϶����ڵ�Q��ʹ��PQ��1����ô�Ƶ�P���߶�AB��������������
��1�����жϵ�D��4.5��2.5���Ƿ����߶�AB��������������
��2�������H ��m��n����һ�κ���![]() ��ͼ���ϣ������߶�AB����������������m��ȡֵ��Χ��
��ͼ���ϣ������߶�AB����������������m��ȡֵ��Χ��
��3�����һ�κ���y=x+b��ͼ�������ٴ���һ����������������ֱ��д��b��ȡֵ��Χ��
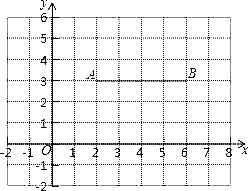
���𰸡���1����D��4.5��2.5�����߶�AB�ġ������㡱��
��2��m��ȡֵ��Χ��![]() ��
��
��3��b��ȡֵ��Χ��![]()
��������
��1����P���߶�AB�ġ������㡱�Ķ��弴���ж�.
��2���������ֱ��y=![]() x-2���߶�AB���ڣ�
x-2���߶�AB���ڣ�![]() ��3���֢ٵ�m��
��3���֢ٵ�m��![]() ʱ���г�����ʽ���ɽ������.
ʱ���г�����ʽ���ɽ������.
��3����ͼ����Rt��AMN�У�AM=1����MAN=45�㣬���M���꣨2-![]() ��3+
��3+![]() ������Rt��BEF�У�BE=1����EBF=45�㣬���E���꣨6+
������Rt��BEF�У�BE=1����EBF=45�㣬���E���꣨6+![]() ��3-
��3-![]() ����
����
�ֱ����ֱ�߾�����M��Eʱ��b��ֵ�����ɽ������.
�⣺��1���ߵ�D���߶�AB�ľ�����0.5��
��0.5<1��
���D��4.5��2.5���Ƿ����߶�AB�ġ������㡱��
��2���ߵ�H��m��n���߶�AB�ġ����ӵ㡱����H��m��n����ֱ��y=![]() x-2�ϣ�
x-2�ϣ�
��n=![]() m-2��
m-2��
ֱ��y=![]() x-2
x-2![]() �߶�AB���ڣ�
�߶�AB���ڣ�![]() ��3��.
��3��.
�ٵ�m��![]() ʱ����n=
ʱ����n=![]() m-2��3��
m-2��3��
��AB��x�ᣬ���ʱ��H��m��n�����߶�AB�ľ�����n-3.
��0��n-3����![]() ��m��5.
��m��5.
����������![]() ��m��5.
��m��5.
��3����ͼ����Rt��AMN�У�AM=1����MAN=45�㣬���M���꣨2-![]() ��3+
��3+![]() ����
����

��Rt��BEF�У�BE=1����ENF=45�㣬���E���꣨6+![]() ��3-
��3-![]() ����
����
��ֱ��y=x+b������Mʱ��b=1+![]() ����ֱ��y=x+b������Eʱ��b=-3-
����ֱ��y=x+b������Eʱ��b=-3-![]() ��
��
��-3-![]() ��b��1+
��b��1+![]() .
.
���㾦�����⿼��һ�κ����ۺ��⡢�߶�AB�ġ������㡱�Ķ����֪ʶ������Ĺؼ����������⣬ѧ��������ۣ�ѧ����������������⣬�����е�ѹ����.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
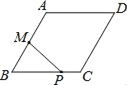
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE.
��1����֤��CE��AD��
��2����DΪAB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3����DΪAB�е㣬��A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ���˵��������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
����һ��˳�������ŵ�һ������Ϊ���У����ڵ�һλ������Ϊ��1���Ϊa1���������ƣ����ڵ�nλ������Ϊ��n���Ϊan��
һ��أ����һ�����дӵڶ�����ÿһ������ǰһ��ıȵ���ͬһ����������ô������н����ȱ����У�������������ȱ����еĹ��ȣ�����ͨ������ĸq��ʾ��q��0�����磺����1��3��9��27����Ϊ�ȱ����У�����a1=1������Ϊq=3��
��1���ȱ�����3��6��12�����Ĺ���qΪ ����4���� ��
��2�����һ������a1��a2��a3��a3�����ǵȱ����У��ҹ���Ϊq����ô���ݶ���ɵõ���
![]() ������
������ ![]() ��
��
��a2=a1q��a3=a2q=��a1q��q=a1q2��a4=a3q=��a1q2��q= a1q3,����
�ɴ˿ɵã�an= ����a1��q�Ĵ���ʽ��ʾ��
��3����һ�ȱ����еĹ���q=2����2����10���������ĵ�1�����4�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������涨һ�������㣺��������������a��b���涨ab��ab+2ab+a�� �磺13��1��3+2��1��3+1��16
��1����3����1����ֵ��
��2������a+1��2��36����a��ֵ��
��3����m��2x��n����![]() x��3������xΪ�����������ԱȽ�m��n�Ĵ�С��
x��3������xΪ�����������ԱȽ�m��n�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=2����B=60�㣬MΪAB���е㣮����P�����εı��ϴӵ�B��������B��C��D�ķ����˶��������Dʱֹͣ������MP�����P�˶���·��Ϊx��MP 2=y�����ʾy��x�ĺ�����ϵ��ͼ�����Ϊ��������
A. 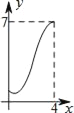 B.
B. 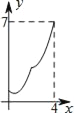 C.
C. 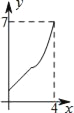 D.
D. 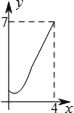
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ź�˾��A��B���ּƷѷ�������ͨ������y��Ԫ����ͨ��ʱ��x�����ӣ��Ĺ�ϵ����ͼ��ʾ������˵������ȷ���ǣ�������
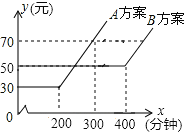
A.��ͨ��ʱ�����200����ѡB��������
B.��ͨ��ʱ�䳬��300����������400����ѡA��������
C.��ͨ������Ϊ70Ԫʱ��A������B������ͨ��ʱ�䳤
D.��ͨ��ʱ����400�����ڣ�B����ͨ������ʼ����50Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
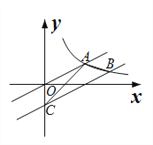
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬OA=3��OB=2����Rt��AOB�Ƶ�O˳ʱ����ת90�����Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90������߶�ED���ֱ���O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ���������_____��
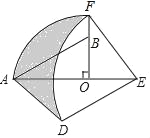
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����в�������һ�˻����������У���ÿ�ִ�Ⱦ��һ�˽�ƽ������x�ˣ�
��1�����һ�ֺ������������ú�x�Ĵ���ʽ��ʾ��
��2���ڽ���ڶ��ִ�Ⱦ֮ǰ������λ���߱���ʱ���벢�������ʵڶ��ִ�Ⱦ���ܹ��Ƿ����21�˻����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() �뷴��������
�뷴��������![]() ��
��![]() ��ͼ���ڵ�A����ֱ������ƽ��4����λ��������������
��ͼ���ڵ�A����ֱ������ƽ��4����λ��������������![]() ��
��![]() ��ͼ���ڵ�B����y���ڵ�C������AB��AC������ABC�����Ϊ_______��
��ͼ���ڵ�B����y���ڵ�C������AB��AC������ABC�����Ϊ_______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com