练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

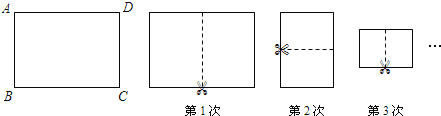
    【题目】将一张长与宽之比为的矩形纸片ABCD进行如下操作：对折并沿折痕剪开，发现每一次所得到的两个矩形纸片长与宽之比都是（每一次的折痕如下图中的虚线所示）．已知AB=1，则第3次操作后所得到的其中一个矩形纸片的周长是 ；第2016次操作后所得到的其中一个矩形纸片的周长是 ．

    【答案】第3次操作后所得到标准纸的周长是：，

    第2016次操作后所得到标准纸的周长为：.

    【解析】

    分别求出每一次对折后的周长，从而得出变化规律求出即可：观察变化规律，得

    第n次对开后所得标准纸的周长=.

    对开次数：

    第一次，周长为：，

    第二次，周长为：，

    第三次，周长为：，

    第四次，周长为：，

    第五次，周长为：，

    第六次，周长为：，

    …

    ∴第3次操作后所得到标准纸的周长是：，

    第2016次操作后所得到标准纸的周长为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知正比例函数y=kx经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为点H，点A的横坐标为3，且△AOH的面积为3．

    （1）求正比例函数的解析式；

    （2）在x轴上能否找到一点P，使△AOP的面积为5？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

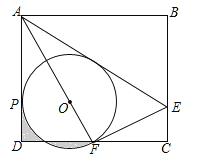
    【题目】（2017四川省达州市，第16题，3分）如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE=CE；④．其中正确结论的序号是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

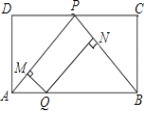
    【题目】如图，矩形ABCD中，P为CD中点，点Q为AB上的动点（不与A，B重合）．过Q作QM⊥PA于M，QN⊥PB于N．设AQ的长度为x，QM与QN的长度和为y．则能表示y与x之间的函数关系的图象大致是（　）

    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=Rt∠，以BC为直径的⊙O交AB于点D，切线DE交AC于点E．

    （1）求证：∠A=∠ADE；

    （2）若AD=16，DE=10，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

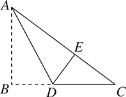
    【题目】如图，有一块Rt△ABC的纸片，∠ABC=900,AB＝6，BC＝8，将△ABC沿AD折叠，使点B落在AC上的E处，则BD的长为( )

    A.3B.4C.5D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．

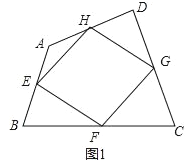
    （1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；

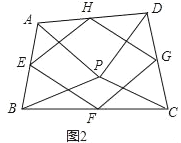
    （2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；

    （3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学将某班级毕业升学体育测试成绩（满分30分）统计整理，得到下表，则下列说法错误的是（　　）

    分数

    20

    21

    22

    23

    24

    25

    26

    27

    28

    人数

    2

    4

    3

    8

    10

    9

    6

    3

    1

    A. 该组数据的众数是24分

    B. 该组数据的平均数是25分

    C. 该组数据的中位数是24分

    D. 该组数据的极差是8分

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】7 月 9 日，滴滴发布北京市滴滴网约车价格调整，公布了新的滴滴快车计价规则，车费由“总里程费＋总时长费”两部分构成，不同时段收费标准不同，具体收费标准如下表，如果车费不足起步价，则按起步价收费.

    时间段

    里程费（元/千米）

    时长费（元/分钟）

    起步价（元）

    06:00-10:00

    1.80

    0.80

    14.00

    10:00-17:00

    1.45

    0.40

    13.00

    17:00-21:00

    1.50

    0.80

    14.00

    21:00-6:00

    2.15

    0.80

    14.00

    (1)小明早上 7:10 乘坐滴滴快车上学，行车里程 6 千米，行车时间 10 分钟，则应付车费多少元?

    (2)小云 17:10 放学回家，行车里程 1 千米，行车时间 15 分钟，则应付车费多少元?

    (3)下晚自习后小明乘坐滴滴快车回家，20:45 在学校上车，由于堵车，平均速度是 a 千米/小时，15 分钟后走另外一条路回家，平均速度是 b 千米/小时，5 分钟后到家，则他应付车费多少元?

    查看答案和解析>>

    同步练习册答案