
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算.比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求3⊕(﹣2)的值;
(2)若3⊕x的值小于16,求x的取值范围,并在数轴上表示出来.
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;④一组对边相等,一组对角相等的四边形是平行四边形.其中正确的命题是_________________(将命题的序号填上即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与运用:
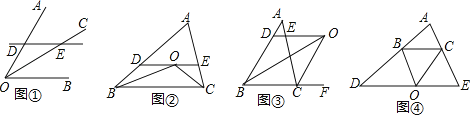
(1)基本图形:如图①,已知OC是∠AOB的角平分线,DE∥OB,分别交OA、OC于点D、E.求证:DE=OD;
(2)在图②中找出这样的基本图形,并利用(1)中的规律解决这个问题:已知△ABC中,两个内角∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,交AB、AC于点D、E.求证:DE=BD+CE;
(3)若将图②中两个内角的角平分线改为一个内角(如图③,∠ABC)、一个外角(∠ACF)和两个都是外角(如图④∠DBC、∠BCE)的角平分线,其它条件不变,则线段DE、BD、CE的数量关系分别是:图③为 、图④为 :并从中任选一个结论证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
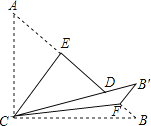
【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边Ac沿CE翻折,使点A落在AB上的D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点F处,两条折痕与斜边AB分别交于点E、F,则线段BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com