
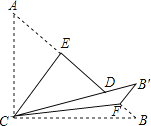
【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边Ac沿CE翻折,使点A落在AB上的D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点F处,两条折痕与斜边AB分别交于点E、F,则线段BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B.
【解析】
试题分析:首先根据折叠可得CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,然后求得△ECF是等腰直角三角形,进而求得∠B′FD=90°,CE=EF=![]() ,ED=AE=
,ED=AE=![]() ,从而求得B′D=1,DF=
,从而求得B′D=1,DF=![]() ,在Rt△B′DF中,由勾股定理即可求得B′F的长,进而得出BF的长.
,在Rt△B′DF中,由勾股定理即可求得B′F的长,进而得出BF的长.
解:根据折叠的性质可知CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,
∴B′D=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC=![]() AC×BC=
AC×BC=![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根据勾股定理求得AB=5,
∴CE=![]() ,
,
∴EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
∴DF=EF﹣ED=![]() ,
,
∴B′F=![]() .
.
∴BF=B'F=![]() ,
,
故选B.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算.比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求3⊕(﹣2)的值;
(2)若3⊕x的值小于16,求x的取值范围,并在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
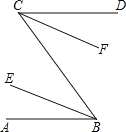
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:
∵AB∥CD,(已知)
∴∠ =∠ .( )
∵ ,(已知)
∴∠EBC=![]() ∠ABC,(角的平分线定义)
∠ABC,(角的平分线定义)
同理,∠FCB= ![]() ∠BCD .
∠BCD .
∴∠EBC=∠FCB.(等式性质)
∴BE∥CF.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一纸箱中装有5个只有颜色不同的球,其中2个白球,3个红球.
(1)求从箱中随机取出一个白球的概率是 ;
(2)若往装有5个球的原纸箱中,再放入x个白球和y个红球,从箱中随机取出一个白球的概率是![]() ,则y与x的函数解析式为 .
,则y与x的函数解析式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com