
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.

【答案】(1)PM与⊙O相切,理由见解析;(2)![]() .
.
【解析】
(1)连接DO并延长交PM于E,如图,利用折叠的性质得OC=DC,BO=BD,则可判断四边形OBDC为菱形,所以OD⊥BC,△OCD和△OBD都是等边三角形,从而计算出∠COP=∠EOP=60°,接着证明PM∥BC得到OE⊥PM,所以OE=![]() OP,根据切线的性质得到OC⊥PC,则OC=
OP,根据切线的性质得到OC⊥PC,则OC=![]() OP,从而可判定PM是⊙O的切线;
OP,从而可判定PM是⊙O的切线;
(2)先在Rt△OPC中计算出OC=1,然后根据等边三角形的面积公式计算四边形OCDB的面积.
(1)PM与⊙O相切.
理由如下:连接DO并延长交PM于E,如图,
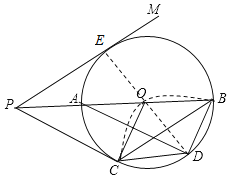
∵弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,
∴OC=DC,BO=BD,
∴OC=DC=BO=BD,
∴四边形OBDC为菱形,
∴OD⊥BC,
∴△OCD和△OBD都是等边三角形,
∴∠COD=∠BOD=60°,
∴∠COP=∠EOP=60°,
∵∠MPB=∠ADC,
而∠ADC=∠ABC,
∴∠ABC=∠MPB,
∴PM∥BC,
∴OE⊥PM,
∴OE=![]() OP,
OP,
∵PC为⊙O的切线,
∴OC⊥PC,
∴OC=![]() OP,
OP,
∴OE=OC,
而OE⊥PC,
∴PM是⊙O的切线;
(2)在Rt△OPC中,OC=![]() PC=
PC=![]() ,
,
∴四边形OCDB的面积=2S△OCD=2×![]() ×12=
×12=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
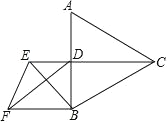
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1、图2、图3,在![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.图1、图2、图3中的
叫做“旋补中心”.图1、图2、图3中的![]() 均是
均是![]() 的“旋补三角形”.
的“旋补三角形”.
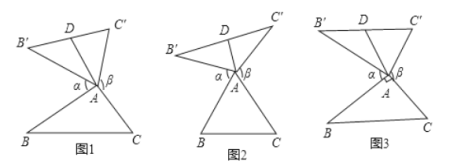
(1)①如图2,当![]() 为等边三角形时,“旋补中线”
为等边三角形时,“旋补中线”![]() 与
与![]() 的数量关系为:
的数量关系为:![]() ______
______![]() ;
;
②如图3,当![]() ,
,![]() 时,则“旋补中线”
时,则“旋补中线”![]() 长为______.
长为______.
(2)在图1中,当![]() 为任意三角形时,猜想“旋补中线”
为任意三角形时,猜想“旋补中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各组条件中,不能说明![]() 的是( )
的是( )
A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() , AD=4.
, AD=4.
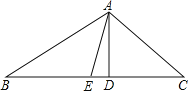
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com