
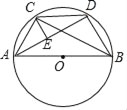
【题目】如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
A. 3﹣![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
先根据勾股定理计算直径AB=![]() =2
=2![]() ,作垂线DP和DQ,根据角平分线的性质得:DP=DQ,由全等可得AP=AQ,设未知数列等式,可得PC和BQ的长,再根据等腰三角形的性质得:∠DEC=∠DCE,根据外角性质得:∠ACE=∠ECB,则∠ACE=∠ECB=45°,作辅助线后可得:△EFC是等腰直角三角形,设EF=FC=a,则CE=
,作垂线DP和DQ,根据角平分线的性质得:DP=DQ,由全等可得AP=AQ,设未知数列等式,可得PC和BQ的长,再根据等腰三角形的性质得:∠DEC=∠DCE,根据外角性质得:∠ACE=∠ECB,则∠ACE=∠ECB=45°,作辅助线后可得:△EFC是等腰直角三角形,设EF=FC=a,则CE=![]() a,AF=2-a,根据△AFE∽△APD,列比例式可得a的值,求CE的长.
a,AF=2-a,根据△AFE∽△APD,列比例式可得a的值,求CE的长.
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=2,BC=4,
∴AB=![]() =2
=2![]() ,
,
∵CD=BD,
∴![]() ,
,
∴∠CAD=∠BAD,
过D作DP⊥AC于P,DQ⊥AB于Q,连接OD,
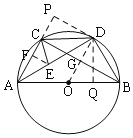
∴PD=DQ,
∴Rt△DPC≌Rt△DQB(HL),
∴CP=BQ,
易得△APD≌△AQD,
∴AP=AQ,
设PC=x,则AP=2+x,AQ=AB-BQ=2![]() -x,
-x,
∴2+x=2![]() -x,
-x,
x=![]() -1,
-1,
∴BQ=CP=![]() -1,OQ=1,
-1,OQ=1,
Rt△ODQ中,DQ=PD=![]() =2,
=2,
∵DE=DC,
∴∠DEC=∠DCE,
∵∠DEC=∠CAD+∠ACE,∠DCE=∠ECB+∠ACE,
∴∠CAD+∠ACE=∠ECB+∠DCB,
∵![]() ,
,
∴∠CAD=∠DCB,
∴∠ACE=∠ECB,
∵∠ACB=90°,
∴∠ACE=∠ECB=45°,
过E作EF⊥AP于F,
∴△EFC是等腰直角三角形,
设EF=FC=a,则CE=![]() a,AF=2-a,
a,AF=2-a,
∵EF∥PD,
∴△AFE∽△APD,
∴![]() ,
,
∴![]() ,
,
∴a=3-![]() ,
,
∴CE=![]() a=
a=![]() (3-
(3-![]() )=3
)=3![]() -
-![]() .
.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)求证:BC平分∠DBE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师在一次“探究性学习”课中,设计了如下数表:
| 2 | 3 | 4 | 5 | … |
| 3 | 8 | 15 | 24 | … |
| 4 | 6 | 8 | 10 | … |
| 5 | 10 | 17 | 26 | … |
由表可知,当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
………
(1)当![]() 时,
时,![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(2)请你分别观察![]() ,
,![]() ,
,![]() 与
与![]() 之间的关系,并分别用含有
之间的关系,并分别用含有![]() 的代数式表示
的代数式表示 ![]() ,
,![]() ,
,![]() .
.
![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(3)猜想以![]() ,
,![]() ,
,![]() 为边的三角形是否为直角三角形,并说明理由.
为边的三角形是否为直角三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
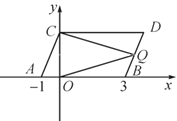
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() □
□![]() □
□![]() □
□![]() ”中的每个“口”内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
”中的每个“口”内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:![]()
(2)若![]() 口
口![]()
![]() 请推算“口”内的运算符号.
请推算“口”内的运算符号.
(3)在“![]() □
□![]() □
□![]() □
□![]() ”的“口”内填入运算符号后,使计算所得的数最小,直接写出这个最小的数.
”的“口”内填入运算符号后,使计算所得的数最小,直接写出这个最小的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CBAC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() (k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则
(k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则![]() _________
_________![]() (填“>”“=”或“<”),若
(填“>”“=”或“<”),若![]() =2,则函数解析式为_________.
=2,则函数解析式为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com