
【题目】已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CBAC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.

【答案】(1)-1;(2)①﹣1+t;②121;③线段CB与AC相等,理由详见解析.
【解析】
(1)依据条件即可得到点A表示﹣6,点B表示﹣6+10=4,再根据点C是线段AB的中点,即可得出点C表示的数;
(2)依据点C表示的数为﹣1,点以每秒1cm的速度向右移动,即可得到运动t秒时,点C表示的数是﹣1+t;
②依据点A表示的数为﹣6﹣2×2=﹣10,点B表示的数为4+4×2=12,点C表示的数是﹣1+2=1,即可得到CBAC的值;
③依据点A表示的数为﹣6﹣2t,点B表示的数为4+4t,点C表示的数是﹣1+t,即可得到点A、B、C在运动的过程中,线段CB与AC相等.
解:(1)∵一个点从数轴上的原点开始,先向左移动6cm到达A点,再从A点向右移动10cm到达B点,
∴点A表示﹣6,点B表示﹣6+10=4,
又∵点C是线段AB的中点,
∴点C表示的数为![]() =﹣1,
=﹣1,
故答案为:﹣1.
(2)①∵点C表示的数为﹣1,点以每秒1cm的速度向右移动,
∴运动t秒时,点C表示的数是﹣1+t,
故答案为:﹣1+t;
②由题可得,当t=2秒时,点A表示的数为﹣6﹣2×2=﹣10,点B表示的数为4+4×2=12,点C表示的数是﹣1+2=1,
∴当t=2秒时,AC=11,BC=11,
∴CBAC=121,
故答案为:121;
③点A、B、C在运动的过程中,线段CB与AC相等.理由:
由题可得,点A表示的数为﹣6﹣2t,点B表示的数为4+4t,点C表示的数是﹣1+t,
∴BC=(4+4t)﹣(﹣1+t)=5+3t,AC=(﹣1+t)﹣(﹣6﹣2t)=5+3t,
∴点A、B、C在运动的过程中,线段CB与AC相等.


科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,建立如图所示的直角坐标系,已知两点A(0,2),B(4,1)
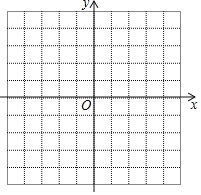
(1)请在x轴上画出一点P,使得PA+PB的值最小;
(2)请直接写出:点P的坐标 ;PA+PB的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式![]() 的最小值.方法如下:
的最小值.方法如下:
解:![]()
![]()
![]()
∵![]() ,得
,得![]() ,
,
∴代数式![]() 的最小值是4.
的最小值是4.
请根据上述材料,解决下列问题:
(1)求代数式![]() 的最小值.
的最小值.
(2)用配方法求代数式![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() , AD=4.
, AD=4.
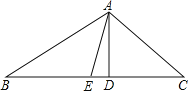
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com