【题目】观察下列等式，
，
，
，
，
，
，
……解答下列问题：
的末位数字是___________．
【答案】2
【解析】
通过观察31=3，32=9，33=27，34=81，35=243，36=729，37=2187…，对前面几个数相加，可以发现末位数字分别是3，2，9，0，3，2，9，0，可知每四个为一个循环，从而可以求得到3+32+33+34+…+32018的末位数字是多少．
∵31=3，32=9，33=27，34=81，35=243，36=729，37=2187…，
∴3=3
3+9=12，
12+27=39，
39+81=120
120+243=363，
363+729=1092，
1092+2187=3279，
又∵2018÷4=504…2，
∴3+32+33+34+…+32018的末位数字是2，
故答案为：2
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图,∠1+∠2=180°，∠DAE=∠BCF，DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)求证：BC平分∠DBE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，一个点从数轴上的原点开始．先向左移动6cm到达A点，再从A点向右移动10cm到达B点，点C是线段AB的中点．
（1）点C表示的数是 ；
（2）若点A以每秒2cm的速度向左移动，同时C、B两点分别以每秒1cm、4cm的速度向右移动，设移动时间为t秒，
①运动t秒时，点C表示的数是 （用含有t的代数式表示）；
②当t＝2秒时，CBAC的值为 ．
③试探索：点A、B、C在运动的过程中，线段CB与AC总有怎样的数量关系？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为【 】
A．1 B．
C． 2 D．
＋1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】材料阅读：若一个整数能表示成a2＋b2(a、b是正整数)的形式，则称这个数为“完美数”．例如：因为13＝32＋22，所以13是“完美数”；再如：因为a2＋2ab＋2b2＝(a＋b)2＋b2(a、b是正整数)，所以a2＋2ab＋2b2也是“完美数”．
(1)请你写出一个大于20小于30的“完美数”，并判断53是否为“完美数”；
(2)试判断(x2＋9y2)·(4y2＋x2)(x、y是正整数)是否为“完美数”，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.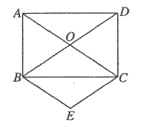
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】函数y=
(k＞0)的图象上两点A(x1, y1)和B(x2, y2),且x1＞x2＞0，分别过A、B向x轴作AA1⊥x轴于A1，BB1⊥x轴于B1，则
_________
(填“＞”“=”或“＜”)，若
=2，则函数解析式为_________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明站在池塘边的
点处，池塘的对面（小明的正北方向）
处有一棵小树，他想知道这棵树距离他有多远，于是他向正东方向走了12步到达电线杆
旁，接着再往前走了12步，到达
处，然后他改向正南方向继续行走，当小明看到电线杆、小树与自己现处的位置
在一条直线上时，他共走了60步.
（1）根据题意，画出示意图（写出作图步骤）；
（2）如果小明一步大约40 
，估算出小明在点处时小树与他的距离为多少米，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小峰和小轩用两枚质地均匀的骰子做游戏，规则如下：每人随机掷两枚骰子一次（若掷出的两枚骰子摞在一起，则重掷），点数和大的获胜；点数和相同为平局．
依据上述规则，解答下列问题：
（1）随机掷两枚骰子一次，用列表法求点数和为2的概率；
（2）小峰先随机掷两枚骰子一次，点数和是7，求小轩随机掷两枚骰子一次，胜小峰的概率．
（骰子：六个面分别刻有1、2、3、4、5、6个小圆点的立方块．点数和：两枚骰子朝上的点数之和．）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com