
【题目】阅读材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式![]() 的最小值.方法如下:
的最小值.方法如下:
解:![]()
![]()
![]()
∵![]() ,得
,得![]() ,
,
∴代数式![]() 的最小值是4.
的最小值是4.
请根据上述材料,解决下列问题:
(1)求代数式![]() 的最小值.
的最小值.
(2)用配方法求代数式![]() 的最值.
的最值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的电脑,已知购买一台A型电脑需0.6万元,购买一台B型电脑需0.4万元,该公司准备投入资金y万元,全部用于购进35台这两种型号的电脑,设购进A型电脑x台.
(1)求y关于x的函数解析式;
(2)若购进B型电脑的数量不超过A型电脑数量的2倍,则该公司至少需要投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
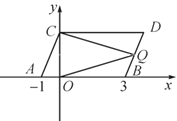
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,公路PQ上A处距O点240米,如果火车行驶时,周围200米以内会受到噪音的影响,那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,求A处受噪音影响的时间。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CBAC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
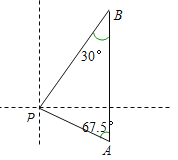
【题目】马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为【 】

A.1 B.![]() C. 2 D.
C. 2 D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.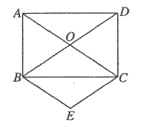
查看答案和解析>>
科目:初中数学 来源: 题型:
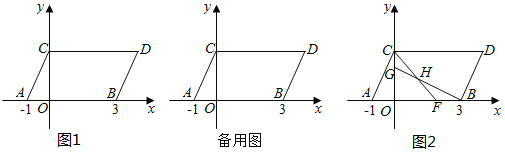
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A、B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C、D,连接AC,BD,CD.
(1)点C的坐标是 ,点D的坐标是 .
(2)在坐标轴上是否存在一点P,S△PAC=![]() S四边形ABDC,若存在这样一点,请求出点P的坐标,若不存在,试说明理由.
S四边形ABDC,若存在这样一点,请求出点P的坐标,若不存在,试说明理由.
(3)如图2,在线段CO上取一点G,使OG=3CG在线段OB上取一点F,使OF=2BF,CF与BG交于点H,求四边形OGHF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com