
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A、B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C、D,连接AC,BD,CD.
(1)点C的坐标是 ,点D的坐标是 .
(2)在坐标轴上是否存在一点P,S△PAC=![]() S四边形ABDC,若存在这样一点,请求出点P的坐标,若不存在,试说明理由.
S四边形ABDC,若存在这样一点,请求出点P的坐标,若不存在,试说明理由.
(3)如图2,在线段CO上取一点G,使OG=3CG在线段OB上取一点F,使OF=2BF,CF与BG交于点H,求四边形OGHF的面积.
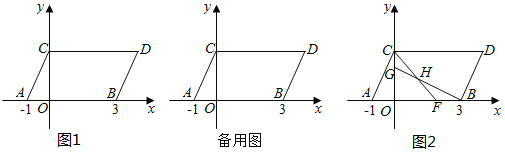
【答案】(1)(0,2),(4,2);(2)存在,点P的坐标为(﹣3,0)或(1,0)或(0,6)或(0,﹣2);(3)![]() .
.
【解析】
(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可;
(2)先根据平行四边形的面积公式求出S四边形ABDC=8,然后分点P在x轴上时求出AP的长度,分两种情况写出点P的坐标;点P在y轴上时,求出CP的长,分两种情况写出点P的坐标;
(3)求出点G、F的坐标,利用待定系数法求出直线CF、BG的解析式,联立求出点H的坐标,再根据S四边形OGHF=S△OBG﹣S△HBF列式计算即可得出结果.
解:(1)∵点A(﹣1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,
∴点C、D的坐标分别为(0,2),(4,2),
故答案为:(0,2),(4,2);
(2)∵点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A、B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C、D,
∴四边形ABCD是平行四边形,AB=4,
∵C(0,2),
∴OC=2,
∴S四边形ABDC=4×2=8,
点P在x轴上时,∵S△PAC=![]() S四边形ABDC,
S四边形ABDC,
∴![]() AP×2=
AP×2=![]() ×8,
×8,
解得AP=2,
当点P在点A的左边时,﹣1﹣2=﹣3,
点P的坐标为(﹣3,0),
点P在点A的右边时,﹣1+2=1,
点P的坐标为(1,0);
点P在y轴上时,∵S△PAC=![]() S四边形ABDC,
S四边形ABDC,
∴![]() CP×1=
CP×1=![]() ×8,
×8,
解得CP=4,
点P在点C的上方时,2+4=6,
点P的坐标为(0,6),
点P在点C的下方时,2﹣4=﹣2,
点P的坐标为(0,﹣2),
综上所述,点P的坐标为(﹣3,0)或(1,0)或(0,6)或(0,﹣2);
(3))∵OG=3CG,
∴OG=![]() OC=
OC=![]() ×2=
×2=![]() ,
,
∴点G的坐标为(0,![]() ),
),
∵B(3,0),
∴OB=3,
∵OF=2BF,
∴OF=![]() OB=
OB=![]() ×3=2,
×3=2,
∴点F的坐标为(2,0),
设直线CF的解析式为:y=kx+a,
则![]() ,
,
解得: ![]() ,
,
∴直线CF的解析式为:y=﹣x+2,
设直线BG的解析式为:y=mx+n,
则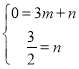 ,
,
解得: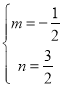 ,
,
∴直线BG的解析式为:y=﹣![]() x+
x+![]()
联立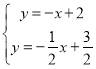 ,
,
解得:![]() ,
,
∴点H的坐标为(1,1),
∴S四边形OGHF=S△OBG﹣S△HBF
=![]() ×3×
×3×![]() ﹣
﹣![]() ×(3﹣2)×1
×(3﹣2)×1
=![]() ﹣
﹣![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式![]() 的最小值.方法如下:
的最小值.方法如下:
解:![]()
![]()
![]()
∵![]() ,得
,得![]() ,
,
∴代数式![]() 的最小值是4.
的最小值是4.
请根据上述材料,解决下列问题:
(1)求代数式![]() 的最小值.
的最小值.
(2)用配方法求代数式![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD,试求一次函数和反比例函数的解析式.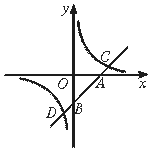
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
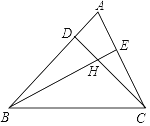
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信付款、转账.把微信账户里的钱转到银行卡叫做提现,自2016年3月1日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,超出的部分需支付0.1%的手续费,以后每次提现支付的手续费均为提现金额的0.1%,
(1)小明用自己的微信账户第一次提现金额为1500元,需支付手续费 元.
(2)小丽使用微信至今,用自己的微信账户共提现三次,提现金额和手续费如下:
第一次 | 第二次 | 第三次 | |
提现金额 | a | b | 2a+3b |
手续费/元 | 0 | 0.2 | 3.1 |
求小丽前两次提现的金额分别为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只渔船在灯塔C的正西方向10海里的A处,以20海里/时的速度沿北偏东30°方向行驶.
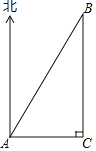
(1)多长时间后,渔船距灯塔最近?
(2)多长时间后,渔船行驶到灯塔的正北方向?此时渔船距灯塔有多远?(其中:202-102=17.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com