
【题目】如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD,试求一次函数和反比例函数的解析式.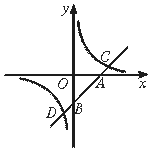
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
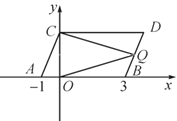
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为【 】

A.1 B.![]() C. 2 D.
C. 2 D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.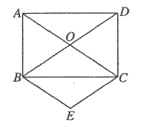
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() (k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则
(k>0)的图象上两点A(x1, y1)和B(x2, y2),且x1>x2>0,分别过A、B向x轴作AA1⊥x轴于A1,BB1⊥x轴于B1,则![]() _________
_________![]() (填“>”“=”或“<”),若
(填“>”“=”或“<”),若![]() =2,则函数解析式为_________.
=2,则函数解析式为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批 粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的 粒数m | 96 | 282 | 382 | 570 | 948 | 1912 | 2850 |
发芽的 频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.956 | 0.950 |
则绿豆发芽的概率估计值是( )
A. 0.96 B. 0.95 C. 0.94 D. 0.90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明站在池塘边的![]() 点处,池塘的对面(小明的正北方向)
点处,池塘的对面(小明的正北方向)![]() 处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆
处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆![]() 旁,接着再往前走了12步,到达
旁,接着再往前走了12步,到达![]() 处,然后他改向正南方向继续行走,当小明看到电线杆
处,然后他改向正南方向继续行走,当小明看到电线杆![]() 、小树
、小树![]() 与自己现处的位置
与自己现处的位置![]() 在一条直线上时,他共走了60步.
在一条直线上时,他共走了60步.
(1)根据题意,画出示意图(写出作图步骤);
(2)如果小明一步大约40 ![]() ,估算出小明在点
,估算出小明在点![]() 处时小树与他的距离为多少米,并说明理由.
处时小树与他的距离为多少米,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
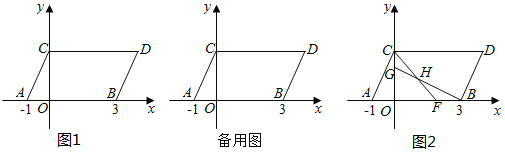
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A、B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C、D,连接AC,BD,CD.
(1)点C的坐标是 ,点D的坐标是 .
(2)在坐标轴上是否存在一点P,S△PAC=![]() S四边形ABDC,若存在这样一点,请求出点P的坐标,若不存在,试说明理由.
S四边形ABDC,若存在这样一点,请求出点P的坐标,若不存在,试说明理由.
(3)如图2,在线段CO上取一点G,使OG=3CG在线段OB上取一点F,使OF=2BF,CF与BG交于点H,求四边形OGHF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AE=![]() (AB+AD);②∠DAB+∠DCB=180;③CD=CB;④S
(AB+AD);②∠DAB+∠DCB=180;③CD=CB;④S![]() S
S![]() =S
=S![]() .其中正确结论的是_________________________.
.其中正确结论的是_________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com