
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
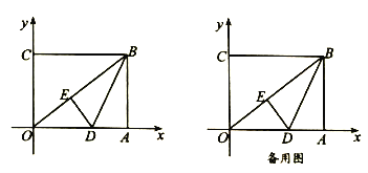
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理即可解决问题;
(2)设AD=x,则OD=OA=AD=12-x,根据轴对称的性质,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根据OE2+DE2=OD2,构建方程即可解决问题;
(3)过点E作EP∥BD交BC于点P,过点P作PQ∥DE交BD于点Q,则四边形DEPQ是平行四边形,再过点E作EF⊥OD于点F,想办法求出最小PE的解析式即可解决问题。
解:(1)在Rt△ABC中,∵OA=12,AB=9,
![]()
故答案为15.
(2)如图,
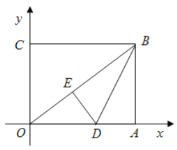
设![]() ,则
,则![]()
根据轴对称的性质,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
设直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]()
则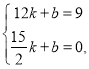 ,
,
解得![]()
∴直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() .
.
故答案为:![]()
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形,再过点
是平行四边形,再过点![]() 作
作![]() 于点
于点![]() ,
,
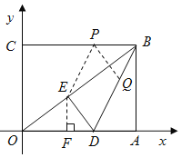
由![]()
得![]() ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() ,
,
又点![]() 在直线
在直线![]() :
:![]() 上,
上,
∴![]() ,解得
,解得![]() ,
,
![]()
由于![]() ,所以可设直线
,所以可设直线![]() ,
,
∵![]() 在直线
在直线![]() 上
上
∴![]() ,解得
,解得![]()
∴直线![]() 为
为![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF的长为( )
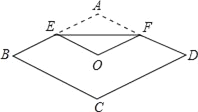
A. 2![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,记
中,记![]() 与
与![]() 的函数
的函数![]() (
(![]() ≠0,n≠0)的图象为图形G, 已知图形G与
≠0,n≠0)的图象为图形G, 已知图形G与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,函数
时,函数![]() 有最小(或最大)值n, 点B的坐标为(
有最小(或最大)值n, 点B的坐标为(![]() ,
, ![]() ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.

(1)如图,若函数![]() 的图象记为图形G,求图形G的伴随直线的表达式;
的图象记为图形G,求图形G的伴随直线的表达式;
(2)如图,若图形G的伴随直线的表达式是![]() ,且伴随四边形的面积为12,求
,且伴随四边形的面积为12,求![]() 与
与![]() 的函数
的函数![]() (m>0,n <0)的表达式;
(m>0,n <0)的表达式;
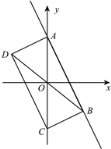
(3)如图,若图形G的伴随直线是![]() ,且伴随四边形ABCD是矩形,求点B的坐标.
,且伴随四边形ABCD是矩形,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
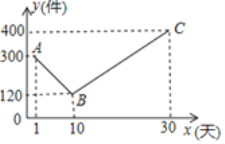
(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
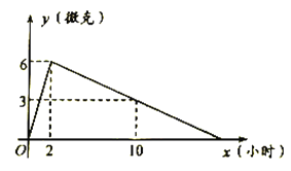
【题目】某医药研究所开发了一种新药,在试验效果时发现,如果成人按规定剂量服用,服药后血液中的含药量逐渐增多,一段时间后达到最大值,接着药量逐步衰减直至血液中含药量为0,每毫升血液中含药量![]() (微克)随时间
(微克)随时间![]() (小时)的变化如图所示,下列说法:(1)2小时血液中含药量最高,达每毫升6微克.(2)每毫升血液中含药量不低于4微克的时间持续达到了6小时.(3)如果一病人下午6:00按规定剂量服此药,那么,第二天中午12:00,血液中不再含有该药,其中正确说法的个数是()
(小时)的变化如图所示,下列说法:(1)2小时血液中含药量最高,达每毫升6微克.(2)每毫升血液中含药量不低于4微克的时间持续达到了6小时.(3)如果一病人下午6:00按规定剂量服此药,那么,第二天中午12:00,血液中不再含有该药,其中正确说法的个数是()
A. 0B. 1
C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
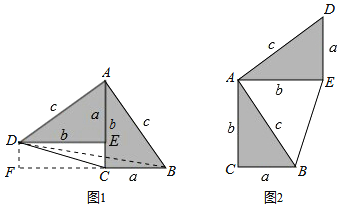
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b-a
S四边形ADCB=![]()
S四边形ADCB=![]()
∴![]() 化简得:a2+b2=c2
化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明,如图(2)中∠DAB=90°,求证:a2+b2=c2
查看答案和解析>>
科目:初中数学 来源: 题型:
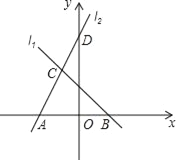
【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com