
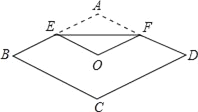
【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF的长为( )
A. 2![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
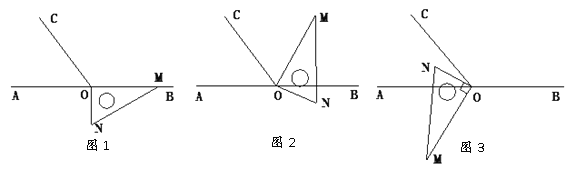
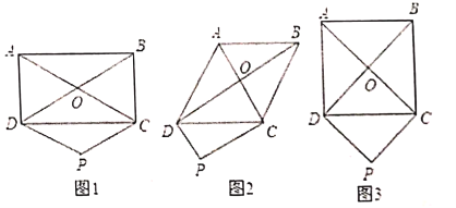
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络视频的兴起让重庆一度成为“网红”城市,并且使得到山城重庆的游客剧增.某旅游公司根据游客的需求推出了“快速游”和“精品游”两种套餐.9月份,该旅游公司“快速游”.“精品游”两种套餐的价格分别为800元/人.2000元/人,其中“快速游”套餐的游客人数比“精品游”套餐的游客人数的2倍多300人,总收入是240万元.
(1)求9月份该旅游公司“快速游”套餐的游客人数;
(2)该公司为了接纳更多的游客,提升口碑,10月份“快速游”套餐价格比9月份下降了![]() ,10月份“精品游”套餐价格比9月份下降了
,10月份“精品游”套餐价格比9月份下降了![]() .已知10月份该公司两种套餐的游客人数的和达到4000人,其中“精品游”套餐的游客人数占两种套餐的游客人数的和的
.已知10月份该公司两种套餐的游客人数的和达到4000人,其中“精品游”套餐的游客人数占两种套餐的游客人数的和的![]() ,且10月份总收入达到了457.6万元,求a的值
,且10月份总收入达到了457.6万元,求a的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.
理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.
探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的![]() ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
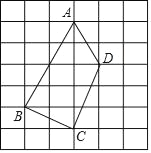
【题目】如图,是大小相等的边长为1的正方形构成的网格,A,B,C,D均为格点.
(Ⅰ)△ACD的面积为_____;
(Ⅱ)现只有无刻度的直尺,请在线段AD上找一点P,并连结BP,使得直线BP将四边形ABCD的面积分为1:2两部分,在图中画出线段BP,并在横线上简要说明你的作图方法._____.
查看答案和解析>>
科目:初中数学 来源: 题型:
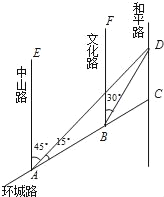
【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图矩形![]() 的对角线
的对角线![]() .
.![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,判断四边形
,判断四边形![]() 的形状并说明理由.
的形状并说明理由.
(2)如果题目中的矩形变为菱形,四边形![]() 的形状____________.
的形状____________.
(3)如果题目中的矩形变为正方形,四边形![]() 的形状____________.
的形状____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
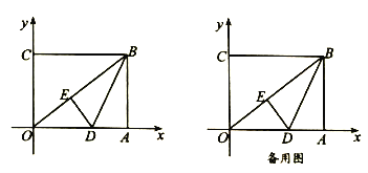
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com