
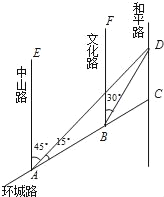
【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
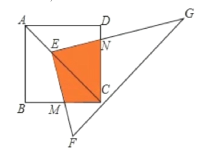
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为6,则重叠部分四边形EMCN的面积为( )
A. 9B. 12C. 16D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,过程如下,请补充完整.
的图象和性质进行了探究,过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 4 |
| 2 | 1 | 0 | 1 | 2 | 3 | 4 | … |
其中,![]() __________.
__________.
(2)根据上表的数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
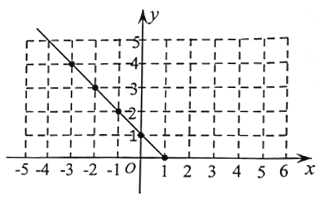
(3)观察图象,写出该函数的两条性质:
①____________________________________________________________
②____________________________________________________________
(4)进一步探究函数图象发现:
①方程![]() 的解是__________.
的解是__________.
②方程![]() 的解是__________.
的解是__________.
③关于![]() 的方程
的方程![]() 有两个不相等实数根,则
有两个不相等实数根,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
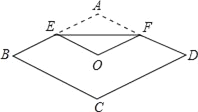
【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF的长为( )
A. 2![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
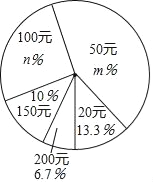
【题目】某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现抽查了九年级(1)班全班同学捐款情况,并绘制出如下的统计表和统计图:
捐款(元) | 20 | 50 | 100 | 150 | 200 |
人数(人) | 4 | 12 | 9 | 3 | 2 |
求:(Ⅰ)m=_____,n=_____;
(Ⅱ)求学生捐款数目的众数、中位数和平均数;
(Ⅲ)若该校有学生2500人,估计该校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
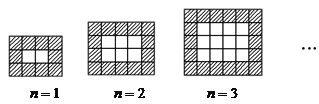
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察各图形并解答有关问题:
(1)在第![]() 个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含
个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含![]() 的代数式表示);
的代数式表示);
(2)设铺设地面所用瓷砖的总块数为![]() ,用(1)中的
,用(1)中的![]() 表示
表示![]() ;
;
(3)当![]() =20时,求
=20时,求![]() 的值;
的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推广“阳光体育”大课间活动,高新中学对已开设的A实心球,B立定跳远,C跑步,D排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:

(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,记
中,记![]() 与
与![]() 的函数
的函数![]() (
(![]() ≠0,n≠0)的图象为图形G, 已知图形G与
≠0,n≠0)的图象为图形G, 已知图形G与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,函数
时,函数![]() 有最小(或最大)值n, 点B的坐标为(
有最小(或最大)值n, 点B的坐标为(![]() ,
, ![]() ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.

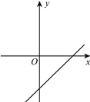
(1)如图,若函数![]() 的图象记为图形G,求图形G的伴随直线的表达式;
的图象记为图形G,求图形G的伴随直线的表达式;
(2)如图,若图形G的伴随直线的表达式是![]() ,且伴随四边形的面积为12,求
,且伴随四边形的面积为12,求![]() 与
与![]() 的函数
的函数![]() (m>0,n <0)的表达式;
(m>0,n <0)的表达式;
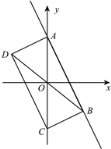
(3)如图,若图形G的伴随直线是![]() ,且伴随四边形ABCD是矩形,求点B的坐标.
,且伴随四边形ABCD是矩形,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
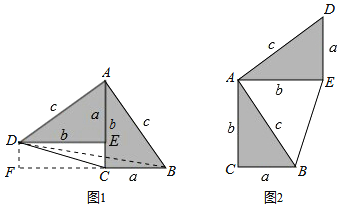
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b-a
S四边形ADCB=![]()
S四边形ADCB=![]()
∴![]() 化简得:a2+b2=c2
化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明,如图(2)中∠DAB=90°,求证:a2+b2=c2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com