
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���![]() ��ͼ������ʽ�����̽�����������£��벹������.
��ͼ������ʽ�����̽�����������£��벹������.
��1���Ա���![]() ��ȡֵ��Χ��ȫ��ʵ����
��ȡֵ��Χ��ȫ��ʵ����![]() ��
��![]() �ļ����Ӧֵ�б����£�
�ļ����Ӧֵ�б����£�
| �� |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | �� |
| �� | 4 |
| 2 | 1 | 0 | 1 | 2 | 3 | 4 | �� |
����![]() __________.
__________.
��2�������ϱ������ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�������˺���ͼ���һ���֣��뻭���ú���ͼ�����һ����.
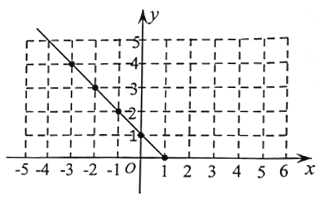
��3���۲�ͼ��д���ú������������ʣ�
��____________________________________________________________
��____________________________________________________________
��4����һ��̽������ͼ���֣�
�ٷ���![]() �Ľ���__________.
�Ľ���__________.
�ڷ���![]() �Ľ���__________.
�Ľ���__________.
�۹���![]() �ķ���
�ķ���![]() �����������ʵ��������
�����������ʵ��������![]() ��ȡֵ��Χ��__________.
��ȡֵ��Χ��__________.
���𰸡���1��3����2������������3���ٺ���ֵy��0����ֵy��0���ڵ�x��1ʱ��y��x�����������4����![]() ����
����![]() ��
��![]() ����
����![]() .
.
��������
��1�����x=-2ʱ�ĺ���ֵ���ɣ�
��2��������㷨��������ͼ�ɣ�
��3�����ͼ��д���������ʼ��ɣ�
��4���ֱ�������̵Ľ⼴�ɽ�����⣻
�⣺��1��x=-2ʱ��y=|x-1|=3����m=3���ʴ�Ϊ3��
��2������ͼ����ͼ��ʾ��
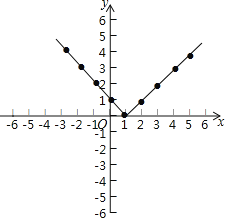
��3���ٺ���ֵy��0���ڵ�x��1ʱ��y��x�����������
�ʴ�Ϊ����ֵy��0����x��1ʱ��y��x�����������
��4���ٷ���|x-1|=0�Ľ���x=1
�ڷ���|x-1|=1.5�Ľ���x=2.5��-0.5
�۹���x�ķ���|x-1|=a������ʵ��������a��ȡֵ��Χ��a��0��
�ʴ�Ϊx=1��x=2.5��-0.5��a��0��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������£�ij���˾��ÿ��ݳ���ʻ![]() Сʱ����ƽ���ٶ�Ϊ
Сʱ����ƽ���ٶ�Ϊ![]() ǧ��ʱ����֪����A�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ������B�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ��
ǧ��ʱ����֪����A�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ������B�ձ������������ʻ2Сʱ��ƽ���ٶȱ����������5ǧ��/ʱ��
��1����A�ճ��˾���������������ʻ����ǧ�ף����ú�![]() ��
��![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����֪A�ճ��˾���������������ʻ120ǧ�ף���B�ճ��˾���������������ʻ����ǧ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() �ĶԽ����ཻ�ڵ�
�ĶԽ����ཻ�ڵ�![]() ����
����![]() ����ô�������������ж��ı���
����ô�������������ж��ı���![]() Ϊƽ���ı��ε��ǣ� ��
Ϊƽ���ı��ε��ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ƶ������������һ�ȳ�Ϊ�����������У�����ʹ�õ�ɽ��������ο;���.ij���ι�˾�����ο͵������Ƴ�������������������Ʒ���������ײ�.9�·ݣ������ι�˾����������.����Ʒ���������ײ͵ļ۸�ֱ�Ϊ800Ԫ/��.2000Ԫ/�ˣ����������������ײ͵��ο�����������Ʒ�����ײ͵��ο�������2����300�ˣ���������240��Ԫ.
(1)��9�·ݸ����ι�˾�����������ײ͵��ο�������
(2)�ù�˾Ϊ�˽��ɸ�����οͣ������ڱ���10�·������������ײͼ۸��9�·��½���![]() ��10�·�����Ʒ�����ײͼ۸��9�·��½���
��10�·�����Ʒ�����ײͼ۸��9�·��½���![]() .��֪10�·ݸù�˾�����ײ͵��ο������ĺʹﵽ4000�ˣ���������Ʒ�����ײ͵��ο�����ռ�����ײ͵��ο������ĺ͵�
.��֪10�·ݸù�˾�����ײ͵��ο������ĺʹﵽ4000�ˣ���������Ʒ�����ײ͵��ο�����ռ�����ײ͵��ο������ĺ͵�![]() ����10�·�������ﵽ��457.6��Ԫ����a��ֵ
����10�·�������ﵽ��457.6��Ԫ����a��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������һ��4��4��4��4�й�16����������ɣ�����������������ѡ�ĸ����������������ĸ��������е��κ���������ͬһ�У�Ҳ����ͬһ�У��кܶ�ѡ������ÿ��ѡ�����ĸ���������ӣ�����Ƕ�ֵ�������е��������е��������ǣ�������
30 |
| 2 | 22 |
��3 | ��2 | �� | 0 |
|��5| | 6 | 23 | |
�� | 4 |
| �� |
A. 5 B. 6 C. 7 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ����ֱ�ǣ�
����ֱ�ǣ�
![]() ��ͼ1�����
��ͼ1�����![]() ����
����![]() �Ķ�����
�Ķ�����
![]() �ҳ�ͼ1����ȵ���ǣ���˵����ȵ����ɣ�
�ҳ�ͼ1����ȵ���ǣ���˵����ȵ����ɣ�
![]() ��ͼ2�У��������ǰ廭һ����
��ͼ2�У��������ǰ廭һ����![]() ��ȵĽǣ�
��ȵĽǣ�
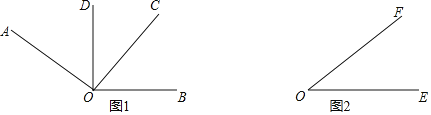
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ǰ������α�һ�����߷ֳɵ����������ν������Ѻ�����������
���ʣ�������������������Ѻ�������������ô�����������ε������ȣ�
���⣺��ͼ�٣��ڡ�ABC�У�CD��AB���ϵ����ߣ���ô��ACD�͡�BCD�����Ѻ���������������S��ACD=S��BCD��
Ӧ�ã���ͼ�ڣ��ھ���ABCD�У�AB=4��BC=6����E��AD�ϣ���F��BC�ϣ�AE=BF��AF��BE���ڵ�O��
��1����֤����AOB�͡�AOE�����Ѻ�����������
��2������OD������AOE�͡�DOE�����Ѻ��������������ı���CDOF�������
̽�����ڡ�ABC�У���A=30�㣬AB=4����D���߶�AB�ϣ�����CD����ACD�͡�BCD�����Ѻ���������������ACD��CD����ֱ�߷��ۣ��õ���A��CD������A��CD���ABC�غϲ��ֵ�������ڡ�ABC�����![]() ����ֱ��д����ABC�������
����ֱ��д����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
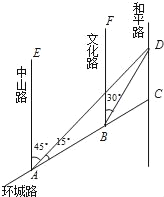
����Ŀ����ͼ��AC��ij�л���·��һ�Σ�AE��BF��CD�����ϱ�����Ľֵ������뻷��·AC�Ľ���·�ڷֱ���A��B��C����������������Dλ�ڵ�A�ı�ƫ��45������B�ı�ƫ��30�������ϣ�AB=2km����DAC=15�㣮
��1����B��D֮��ľ��룻
��2����C��D֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����ABΪֱ���ġ�O�ֱ���BC��AC���ڵ�D��E������D����O������DF����AC�ڵ�F��
��1����֤��DF��AC��
��2������O�İ뾶Ϊ4����CDF��22.5��������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com